Equilateral Triangle Calculator | 60° 60° 60° Triangle Calculator
The Equilateral Triangle Calculator (60° 60° 60° Triangle Calculator) is a free and easy-to-use online tool that helps you quickly calculate all sides and properties of an equilateral triangle based on a single known value. Whether you’re working with the side length, height (altitude), area, or perimeter, simply enter any one value, and the calculator will instantly determine all the remaining dimensions with accuracy and ease.
It also provides clear, step-by-step explanations, making it ideal for learning geometric concepts, verifying your work, or using it as a quick reference tool—conveniently available on CalculationClub.com.
How to Use the Online Equilateral Triangle Calculator
1. Enter Any One Value
Start by entering any one known value of the triangle—such as side length (a), height (h or altitude), area, or perimeter. The calculator only needs one input to compute the rest.
2. Choose Decimal Precision and Units
Select the number of decimal places you’d like the results to display (e.g., 3), and choose your preferred unit of measurement, such as meters (m) :
Then, choose your preferred unit of measurement from the following options:
- Meters (m)
- Centimeters (cm)
- Millimeters (mm)
- Yards (yd)
- Feet (ft)
- Inches (in)
3. View Instant Results
Once you input a value, the calculator instantly determines all remaining dimensions of the equilateral triangle using standard geometric formulas.
4. Show or Hide Steps
Click “Show Steps” to view a detailed explanation of how each value was calculated. You can also click “Hide Steps” for a cleaner, summary-only view.
5. Reset for a New Calculation
Click the “Reset” button to clear all fields and enter a new set of values for another triangle calculation.

Equilateral Triangle Calculator (60° 60° 60° Triangle Calculator)
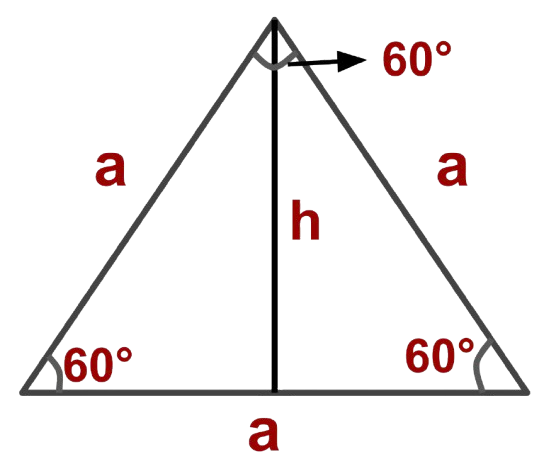
What is an Equilateral Triangle?
An equilateral triangle is a special type of triangle in geometry where all three sides are equal in length and all three interior angles measure exactly 60°. Because of its perfect symmetry, it has unique mathematical properties that make calculations for height, area, and perimeter straightforward using standard formulas.
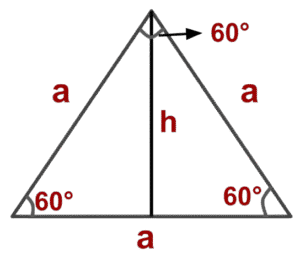
Sides and Properties of an Equilateral Triangle
In an equilateral triangle:
- All sides are equal in length.
- All angles measure 60°, making it both equiangular and equilateral.
- You only need one known value (side, height, area, or perimeter) to calculate the rest.
Standard Notations:
- Side length: a
- Height (altitude): h
- Area: A
- Perimeter: P = 3a
Height (Altitude) of an Equilateral Triangle
The altitude (height) of an equilateral triangle is a line drawn from one vertex perpendicular to the opposite side (base). It splits the triangle into two congruent 30-60-90 right triangles.
Formula for Altitude (h) = $ \mathbf{ a \cdot \frac{\sqrt{3}}{2}}$
Deriving the Altitude Using Sine Function
To find the height of an equilateral triangle using trigonometry:
1. Drop a perpendicular from the top vertex to the base. This bisects the base and splits the equilateral triangle into two 30°-60°-90° right triangles.
2. In this right triangle:
- Hypotenuse = side of the triangle = a
- Angle at the base = 60°
- Opposite side (height) = h
3. Use the sine function:
$\sin(60^\circ)$ $ = \frac{\text{Opposite}}{\text{Hypotenuse}}$ $ = \frac{h}{a}$
4. Rearranging the formula:
$ h = a \cdot \sin(60^\circ)$
5. Substitute the value of $\sin(60^\circ) = \frac{\sqrt{3}}{2}$:
$ \mathbf{h = a \cdot \frac{\sqrt{3}}{2}}$
Summary of an Equilateral Triangle
- All three sides are equal.
- All angles measure exactly 60°.
- The altitude divides the triangle into two 30-60-90 right triangles.
- With one known value, you can determine all other properties.
Formulas: Equilateral Triangle 60°-60°-60°
Side:
In an equilateral triangle, all three sides are equal.
Let each side be aa, then:
- Side 1 = a
- Side 2 = a
- Side 3 = a
Altitude (h):
Drop a perpendicular from the top vertex to the base. This creates two 30°-60°-90° right triangles.
Using the sine function:
$\sin(60^\circ) = \frac{h}{a}$
$h = a \cdot \sin(60^\circ) $
$\sin(60^\circ) = \frac{\sqrt{3}}{2}$
$\mathbf{h = a \cdot \frac{\sqrt{3}}{2}}$
Perimeter (P)
Since all three sides are equal:
P = a + a + a = 3a
P = 3a
Area (A)
$A = \frac{1}{2} \cdot a \cdot h$
$A = \frac{1}{2} \cdot a \cdot \frac{\sqrt{3}}{2}a$
$A = \frac{a^2\sqrt{3}}{4}$
$\mathbf{A = \frac{a^2\sqrt{3}}{4}}$
Problem: Equilateral Triangle (60°-60°-60°)
Example.1 = Given an equilateral triangle with one side $x = 5$ units, we need to find the other sides, height, perimeter, and area of the triangle.
Solution: In an equilateral triangle, all sides are equal, so the other sides are also $x$. Therefore:
$\text{Other Sides} = 5$ $ \text{ units}$
The height $h$ can be calculated using the formula:
$h = \frac{x \sqrt{3}}{2}$ $ = \frac{5 \sqrt{3}}{2}$ $ \approx 4.33 \text{ units}$
The perimeter $P$ is the sum of all three sides:
$P = x + x + x = 3x $ $= 3 \times 5 = 15 \text{ units}$
Finally, the area $A$ of the triangle can be calculated using the formula:
$A = \frac{\sqrt{3}}{4} \times x^2$ $ = \frac{\sqrt{3}}{4} \times 5^2$ $ = \frac{\sqrt{3}}{4} \times 25$ $ \approx 10.83 \text{ square units}$
Example.2 = Given an equilateral triangle with a height $h = 6$ units, we need to find the side length, perimeter, and area of the triangle.
Solution: The height of an equilateral triangle is given by:
$h = \frac{x \sqrt{3}}{2}$
Solving for $x$:
$x = \frac{2h}{\sqrt{3}} = \frac{2 \times 6}{\sqrt{3}} = \frac{12}{\sqrt{3}} \approx 6.93 \text{ units}$
The side length is:
$\text{Side Length} = x = 6.93 \text{ units}$
The perimeter $P$ is:
$P = 3x = 3 \times 6.93 $ $= 20.79 \text{ units}$
The area $A$ is:
$A = \frac{\sqrt{3}}{4} \times x^2$ $ = \frac{\sqrt{3}}{4} \times (6.93)^2$ $ \approx 21.18 \text{ square units}$
Example.3 = Given an equilateral triangle with perimeter $P = 24$ units, we need to find the side length, height, and area of the triangle.
Solution: The perimeter is:
$P = 3x$
Solving for $x$:
$x = \frac{P}{3}$ $ = \frac{24}{3}$ $ = 8 \text{ units}$
The side length is:
$\text{Side Length} = x = 8 \text{ units}$
The height $h$ is:
$h = \frac{x \sqrt{3}}{2} = \frac{8 \sqrt{3}}{2} $ $ = 4 \sqrt{3} \approx 6.93 \text{ units}$
The area $A$ is:
$A = \frac{\sqrt{3}}{4} \times x^2$ $ = \frac{\sqrt{3}}{4} \times 8^2 = \frac{\sqrt{3}}{4} \times 64 $ $\approx 27.71 \text{ square units}$
Example.4 = Given an equilateral triangle with area $A = 36$ square units, we need to find the side length, height, and perimeter.
Solution: The area is:
$A = \frac{\sqrt{3}}{4} \times x^2$
Solving for $x$:
$x^2 = \frac{4A}{\sqrt{3}}$ $ = \frac{4 \times 36}{\sqrt{3}}$ $ = \frac{144}{\sqrt{3}} \approx 83.14$
Taking the square root:
$x \approx \sqrt{83.14} \approx 9.12 \text{ units}$
The side length is:
$\text{Side Length} = x = 9.12 \text{ units}$
The height $h$ is:
$h = \frac{x \sqrt{3}}{2}$ $ = \frac{9.12 \sqrt{3}}{2} \approx 7.91 \text{ units}$
The perimeter $P$ is:
$P = 3x = 3 \times 9.12 = 27.36 \text{ units}$
Frequently Asked Questions on Equilateral Triangle Calculator
1. What is an equilateral triangle?
An equilateral triangle is a special type of triangle where all three sides are of equal length, and each of its angles is 60°.
2. How does the equilateral triangle calculator work?
The calculator uses the property of an equilateral triangle, where all sides are equal. If you input the length of one side, the calculator will automatically compute the area, perimeter, height, and other properties using the formulas specific to equilateral triangles.
3. Which side is which in an equilateral triangle?
In an equilateral triangle, all three sides are of equal length, and each angle is 60°.
4. What is the ratio of the sides in an equilateral triangle?
The sides are all equal, so the ratio of the sides is:
Side : Side : Side = 1 : 1 : 1
5. Can I use any unit for input?
Yes, you can use any unit of measurement as long as you maintain consistency in the units for all sides. The calculator will preserve the same unit in the output.
6. Is this triangle always equilateral?
Yes, by definition, an equilateral triangle is always a triangle with three equal sides and three equal angles of 60° each.
7. What if I enter the length of one side?
The calculator will use the length of the side to automatically calculate the other properties, such as the area, perimeter, and height of the equilateral triangle.
8. Can this calculator show steps or formulas used?
Some versions of the calculator display the formulas used in the background. If yours doesn’t, you can manually apply:
- $\text{Perimeter} = 3 \times \text{side}$
- $\text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2$
- $\text{Height} = \frac{\sqrt{3}}{2} \times \text{side}$
9. Why is this triangle useful in geometry or trigonometry?
Equilateral triangles are fundamental in geometry because of their symmetry and equal side lengths. They are used in various applications such as tiling, tessellation, and creating symmetrical designs in architecture and art.
10. Can I use this calculator for solving real-life problems?
Yes, the calculator can be used for real-life problems involving equilateral triangles, such as designing objects with equal sides, constructing structures with symmetrical properties, or solving trigonometric problems related to equilateral shapes.
Final Thoughts: The Equilateral Triangle Calculator is a simple and reliable tool that helps you easily find all the sides and properties of an equilateral triangle from just one known value. Whether you’re studying, teaching, or working professionally, it’s fast, accurate, and always ready for you on CalculationClub.com.
My Request to All: If you enjoy using my Equilateral Triangle Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
Telegram Link – Join Our Telegram Channel
YouTube Link – Subscribe to Our YouTube Channel
For more tools, please visit our homepage at CalculationClub – Free Online Calculators
For additional tools in Hindi, you can visit MeterToFeet
Thank you for your support!