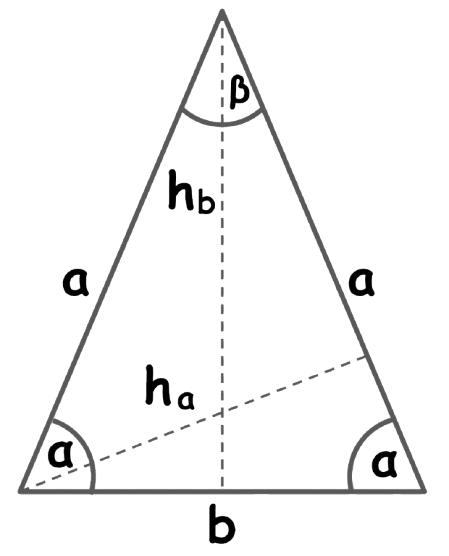
Isosceles Triangle Calculator
The Isosceles Triangle Calculator helps you calculate any unknown value in an isosceles triangle—be it the equal sides (a), base (b), angles α and β, altitudes (ha, hb), area (A), or perimeter (P). Just enter any two known values, and the calculator intelligently applies trigonometric and geometric formulas to solve the rest with step-by-step precision.
This calculator uses formulas specific to isosceles triangles, where two sides are of equal length, and the base connects them. It’s designed for students, teachers, architects, and engineers needing quick and accurate results.
Accepted Input Combinations
You can use a wide variety of input pairs (27 total) to calculate the missing values in an isosceles triangle:
1. Two Sides Given
- a & b (Equal side & Base)
2. Area and One Side
- Area & a
- Area & b
3. Angle and One Side
- a & ∠α
- a & ∠β
- b & ∠α
- b & ∠β
4. Perimeter and One Side
- Perimeter & a
- Perimeter & b
5. Perimeter and Area
- Perimeter & Area
6. Altitude and One Side
- a & Altitude (ha)
- b & Altitude (ha)
- a & Altitude (hb)
- b & Altitude (hb)
7. Altitude and One Angle
- ∠α & Altitude (ha)
- ∠β & Altitude (ha)
- ∠α & Altitude (hb)
- ∠β & Altitude (hb)
8. Area and Altitude
- Area & Altitude (ha)
- Area & Altitude (hb)
9. Both Altitudes
- Altitude (ha) & Altitude (hb)
10. Area and One Angle
- Area & ∠α
- Area & ∠β
11. Perimeter and One Altitude
- Perimeter & Altitude (ha)
- Perimeter & Altitude (hb)
12. Perimeter and One Angle
- Perimeter & ∠α
- Perimeter & ∠β
Outputs Provided by the Calculator
Based on the input combination, the Isosceles Triangle Calculator will compute and display:
- Equal sides (a)
- Base (b)
- Angle α (at base)
- Angle β (at apex)
- Altitude ha (to equal sides)
- Altitude hb (to base)
- Area (A)
- Perimeter (P)
Note: This Isosceles Triangle Calculator supports multiple unit types such as meters (m), centimeters (cm), millimeters (mm), feet (ft), yards (yd), and inches (in). Angles can be entered in either degrees or radians. With smart detection of 27 different input pairings, it’s perfect for all levels of users.
How to Use the Isosceles Triangle Calculator
1. Select Your Input Type: Use the dropdown menu labeled “Given” to choose one of the following 27 supported combinations:
- a & b (Equal side and Base)
- Area & a
- Area & b
- a & ∠α
- a & ∠β
- b & ∠α
- b & ∠β
- Perimeter & a
- Perimeter & b
- Perimeter & Area
- a & Altitude (ha)
- b & Altitude (ha)
- a & Altitude (hb)
- b & Altitude (hb)
- ∠α & Altitude (ha)
- ∠β & Altitude (ha)
- ∠α & Altitude (hb)
- ∠β & Altitude (hb)
- Area & Altitude (ha)
- Area & Altitude (hb)
- Altitude (ha) & Altitude (hb)
- Area & ∠α
- Area & ∠β
- Perimeter & Altitude (ha)
- Perimeter & Altitude (hb)
- Perimeter & ∠α
- Perimeter & ∠β
2. Enter Known Values: Input any two known values depending on your selected combination. This calculator supports calculating key isosceles triangle properties like the equal sides (a), base (b), angles α and β, altitudes ha (to equal sides) and hb (to base), area (A), and perimeter (P). Based on your input, all remaining values will be accurately computed.
3. Choose Decimal Precision:
- Choose the number of decimal places (e.g., 2, 3, or more) for the output values.
- Select Units:
- Length Units: Meters (m), Centimeters (cm), Millimeters (mm), Yards (yd), Feet (ft), Inches (in)
- Angle Units: Degrees (°), Radians (rad)
4. Click “Calculate”: Once you’ve entered the required inputs, press the Calculate button. The calculator will compute all the missing dimensions and angles instantly.
5. Show/Hide Steps: Toggle the “Show Steps” option if you want to see detailed calculation steps or hide them for a cleaner view.
6. Reset: Use the Reset button to clear all inputs and start a fresh calculation.

Isosceles Triangle Calculator
Important Formulas Used in This Isosceles Triangle Calculator
The Isosceles Triangle Calculator uses a variety of geometric and trigonometric formulas to calculate unknown sides, angles, altitudes, perimeter, and area based on two known values. Below are the key formulas applied:
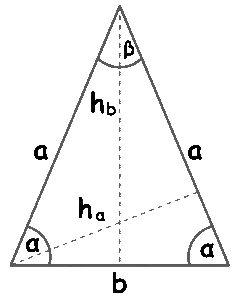
1. Angle Sum of Triangle
$\alpha + \alpha + \beta = 180^\circ$
This formula shows that the sum of interior angles in any triangle is 180°, and in an isosceles triangle, two angles ($\alpha$) are equal.
2. Vertex Angle
$\beta = 180^\circ – 2\alpha$
Used to find the angle opposite the base when base angles are known.
3. Base Angle (when vertex angle is known)
$\alpha = \frac{180^\circ – \beta}{2}$
This formula calculates the base angles when the vertex angle $\beta$ is known in an isosceles triangle.
3. Perimeter of an Isosceles Triangle
$P = 2a + b$
This formula calculates the perimeter of an isosceles triangle, where:
$a$ represents the length of each of the two equal sides, and
$b$ represents the length of the base (the side that is not equal).
By summing the lengths of all three sides, the perimeter gives the total boundary length of the triangle.
4. Area Using Base and Height
$A = \frac{b \times h_b}{2}$
This is the most direct formula where $b$ is the base and $h_b$ is the perpendicular height from the opposite vertex to the base.
5. Area Using Equal Side and Corresponding Height
$A = \frac{a \times h_a}{2}$
When the height from the base angle to the opposite side (equal side $a$) is known, this formula applies.
6. Area Using Trigonometry (Sine of Included Angle)
$h_a = a \times \sin(\beta)$
$A = \frac{1}{2} \times a^2 \times \sin(\beta)$
This formula is useful when one equal side $a$ and the vertex angle $\beta$ are known. It uses the sine rule to calculate height and then the area.
7. Area Using Two Sides and Included Angle
$A = \frac{1}{2} \times a \times b \times \sin(\alpha)$
Applicable when two sides and the included angle $\alpha$ are known (even if triangle is isosceles).
5. Area Using Heron’s Formula
$s = \frac{a + a + b}{2} = \frac{2a + b}{2}$
$A = \sqrt{s(s – a)^2(s – b)}$
Heron’s formula is useful when all three sides are known. This version is simplified for isosceles triangles where two sides are equal ($a = a$).
6. Altitude to Base
Using the Pythagorean Theorem:
$h_b = \sqrt{a^2 – \left(\frac{b}{2}\right)^2}$
Or using sine:
$h_b = a \times \sin(\alpha)$
7. Altitude to Side a
$h_a = \frac{2A}{a}$
Or:
$h_a = b \times \sin(\alpha)$
8. Law of Cosines
$a^2 = b^2 + c^2 – 2bc \cos(\alpha)$
$b^2 = a^2 + c^2 – 2ac \cos(\beta)$
$c^2 = a^2 + b^2 – 2ab \cos(\gamma)$
For Vertex Angle (β):
$b^2 = a^2 + a^2 – 2a^2 \cos(\beta)$
$\cos(\beta) = \frac{2a^2 – b^2}{2a^2}$
Used when both equal sides ($a$) and the base ($b$) are known to calculate the angle opposite the base.
For Base Angle (α):
$a^2 = a^2 + b^2 – 2ab \cos(\alpha)$
$\cos(\alpha) = \frac{a^2 + b^2 – a^2}{2ab} = \frac{b}{2a}$
This simplified form applies in isosceles triangles and helps find the base angle when one side ($a$) and the base ($b$) are known.
9. Law of Sines
$\frac{\sin(\alpha)}{a} = \frac{\sin(\beta)}{b}$
Used when one angle and one side are known.
10. Trigonometric Relations
$\cos(\alpha) = \frac{b}{2a}$
$\sin(\alpha) = \frac{h_b}{a}$
$\tan(\alpha) = \frac{h_b}{b/2}$
11. Angle Conversions
$\text{Radians} = \text{Degrees} \times \frac{\pi}{180}$
$\text{Degrees} = \text{Radians} \times \frac{180}{\pi}$
Note: The calculator dynamically chooses the correct formula based on which pair of values you input (e.g., side + angle, area + base, etc.) to deliver complete and accurate results.
Formula: Find Base from Equal Side and Area
Step 1: Area of Triangle
$A = \frac{1}{2} \cdot b \cdot h$
Solving for height ($h$):
$h = \frac{2A}{b}$
Step 2: Pythagorean Theorem in Right Triangle
Drop a perpendicular from the vertex to the base, which bisects the base into two equal halves:
$a^2 = h^2 + \left(\frac{b}{2}\right)^2$
Substituting $h = \frac{2A}{b}$:
$a^2 = \left(\frac{2A}{b}\right)^2 + \left(\frac{b}{2}\right)^2$
Step 3: Simplify and Rearrange
$a^2 = \frac{4A^2}{b^2} + \frac{b^2}{4}$
Multiply both sides by $b^2$:
$a^2 b^2 = 4A^2 + \frac{b^4}{4}$
Multiply everything by 4:
$4a^2 b^2 = 16A^2 + b^4$
Step 4: Solve Quadratic in $b^2$
Rearranged as:
$b^4 – 4a^2 b^2 + 16A^2 = 0$
Let $x = b^2$, solve quadratic:
$x = 2a^2 \pm 2\sqrt{a^4 – 4A^2}$
So,
$b^2 = 2a^2 – 2\sqrt{a^4 – 4A^2}$
Final Formula:
$\boxed{b = \sqrt{2a^2 – \sqrt{4a^4 – 16A^2}}}$
This formula calculates the base ($b$) of an isosceles triangle when you know the equal side ($a$) and the area ($A$).
Formula: Find Base from Perimeter and Base Angle
Step 1: Perimeter of Isosceles Triangle
The perimeter ($P$) is the sum of all sides:
$P = 2a + b$
Step 2: Express Equal Side ($a$) Using Base Angle ($\alpha$)
From the Law of Cosines or right triangle formed by dropping altitude:
$a = \frac{b}{2 \cos(\alpha)}$
Since $\sec(\alpha) = \frac{1}{\cos(\alpha)}$, this becomes:
$a = \frac{b}{2} \times \sec(\alpha)$
Step 3: Substitute $a$ in the Perimeter Formula
Replace $a$ in $P = 2a + b$:
$P = 2 \times \left(\frac{b}{2} \sec(\alpha)\right) + b $$= b \sec(\alpha) + b$
Factor $b$:
$P = b (\sec(\alpha) + 1)$
Step 4: Solve for Base ($b$)
Rearranged:
$b = \frac{P}{1 + \sec(\alpha)}$
Final Formula:
$\boxed{b = \frac{P}{1 + \sec(\alpha)}}$
This formula calculates the base ($b$) of an isosceles triangle when the perimeter ($P$) and the base angle ($\alpha$) are known.
Formula: Find Base from Two Altitudes ($h_a$ and $h_b$)
Step 1: Use basic height formulas
From two different area expressions of the isosceles triangle:
- $A = \frac{1}{2} \cdot b \cdot h_b$ (using base $b$ and height to base $h_b$)
- $A = \frac{1}{2} \cdot a \cdot h_a$ (using equal side $a$ and corresponding height $h_a$)
Step 2: Eliminate area ($A$)
Set both area expressions equal:
$\frac{1}{2} \cdot b \cdot h_b = \frac{1}{2} \cdot a \cdot h_a$
Simplify:
$b \cdot h_b = a \cdot h_a$
Solve for $a$:
$a = \frac{b \cdot h_b}{h_a}$
Step 3: Apply Pythagoras on half base
Drop perpendicular from vertex to base, forming a right triangle:
$h_b^2 + \left(\frac{b}{2}\right)^2 = a^2$
Substitute $a$:
$h_b^2 + \left(\frac{b}{2}\right)^2 = \left(\frac{b \cdot h_b}{h_a}\right)^2$
Step 4: Expand and simplify
Left side:
$h_b^2 + \frac{b^2}{4}$
Right side:
$\frac{b^2 h_b^2}{h_a^2}$
Now equate both:
$h_b^2 + \frac{b^2}{4} = \frac{b^2 h_b^2}{h_a^2}$
Step 5: Multiply through by $h_a^2$ and rearrange
$h_a^2 h_b^2 + \frac{b^2 h_a^2}{4} = b^2 h_b^2$
Move all terms to one side:
$h_a^2 h_b^2 = b^2 \left(h_b^2 – \frac{h_a^2}{4}\right)$
Solve for $b^2$:
$b^2 = \frac{h_a^2 h_b^2}{h_b^2 – \frac{h_a^2}{4}}$
Take square root:
$b = \frac{h_a h_b}{\sqrt{h_b^2 – \frac{h_a^2}{4}}}$
Multiply numerator and denominator by 2:
$\boxed{b = \frac{2 h_a h_b}{\sqrt{4 h_b^2 – h_a^2}}}$
Final Formula:
$\boxed{b = \frac{2 h_a h_b}{\sqrt{4 h_b^2 – h_a^2}}}$
This formula calculates the base ($b$) of an isosceles triangle when both altitudes — $h_a$ (to equal side) and $h_b$ (to base) — are known.
Formula: Find Equal Side from Perimeter and Height to Base
Step 1: Perimeter of Isosceles Triangle
$P = 2a + b \Rightarrow b = P – 2a$
Step 2: Use Pythagoras Theorem
Drop a perpendicular from vertex to base. Half the base becomes $\frac{b}{2}$:
$a^2 = h_b^2 + \left(\frac{b}{2}\right)^2$
Substitute $b = P – 2a$:
$a^2 = h_b^2 + \left(\frac{P – 2a}{2}\right)^2$
Step 3: Expand Right Side
$a^2 = h_b^2 + \frac{(P – 2a)^2}{4}$
$a^2 = h_b^2 + \frac{P^2 – 4Pa + 4a^2}{4}$
Step 4: Multiply Entire Equation by 4
$4a^2 = 4h_b^2 + P^2 – 4Pa + 4a^2$
Subtract \(4a^2\) from both sides:
$0 = 4h_b^2 + P^2 – 4Pa$
Step 5: Solve for \(a\)
$4Pa = P^2 + 4h_b^2$
$a = \frac{P^2 + 4h_b^2}{4P}$
Final Formula:
$\boxed{a = \frac{P^2 + 4h_b^2}{4P}}$
This gives the length of equal side \(a\) when perimeter \(P\) and height to base \(h_b\) are known.
Formula: Find Base from Perimeter (P) and Height to Equal Side (ha)
Step 1: Express Equal Side a using Perimeter
In an isosceles triangle: \(P = 2a + b\)
Solve for \(a\):
$a = \frac{P – b}{2}$
Step 2: Use Trigonometric Identity for Sine
Drop perpendicular from angle to equal side \(a\):
$\sin(\alpha) $$= \frac{h_a}{b} \Rightarrow h_a $$= b \cdot \sin(\alpha)$
From cosine rule:
$\cos(\alpha) $$= \frac{b}{2a} $$= \frac{b}{P – b}$
Then:
$\sin^2(\alpha) $$= 1 – \cos^2(\alpha) $$= 1 – \left(\frac{b}{P – b}\right)^2$
Substitute into \(h_a^2 = b^2 \cdot \sin^2(\alpha)\):
$h_a^2 $$= b^2 \left(1 – \left(\frac{b}{P – b}\right)^2\right)$
Step 3: Multiply both sides by \((P – b)^2\)
$h_a^2 (P – b)^2 $$= b^2 (P – b)^2 – b^4$
Step 4: Expand both sides
Left:
$h_a^2 P^2 – 2P h_a^2 b + h_a^2 b^2$
Right:
$b^2 P^2 – 2P b^3 + b^2 b^2 – b^4$ (simplifies to previous form)
Step 5: Rearrange all terms to one side
$2b^3 P + b^2 (h_a^2 – P^2) -$$ 2b P h_a^2 + P^2 h_a^2 = 0$
Final Cubic Equation:
$\boxed{2b^3 P + b^2 (h_a^2 – P^2) -$$ 2b P h_a^2 + P^2 h_a^2 = 0}$
Use this cubic to find base \(b\) when perimeter \(P\) and height to side \(h_a\) are known.
FAQs on Isosceles Triangle Calculator
1. What values do I need to use the Isosceles Triangle Calculator?
You only need to input **any two known values**—such as side lengths, angles, area, perimeter, or altitude. The calculator automatically applies geometric and trigonometric formulas to compute the remaining dimensions of the isosceles triangle.
2. Can I calculate the triangle if I only know the area and one side?
Yes. The calculator allows you to select combinations like Area & a, Area & b, or Area & c. Based on your selection, it uses area formulas (like \( A = \frac{1}{2} \times b \times h \)) to determine all unknown values.
3. What if I only know one angle and one side?
That’s not a problem! Choose an option like a & ∠α, b & ∠β, or any other valid pair. The calculator will then apply sine, cosine, or angle sum rules to calculate the triangle’s full geometry.
4. Does the calculator show the step-by-step process?
Yes. There is a “Show/Hide Steps” option. When enabled, the calculator displays detailed calculation steps using relevant formulas so users can understand how the results were derived.
5. Can I change units or decimal precision in the calculator?
Absolutely. You can select your preferred length units (like cm, m, ft, in) and angle units (degrees or radians). You can also set how many decimal places the results should display—for precise or rounded answers.
Final Thoughts: Isosceles Triangle Calculator quickly solves for sides, angles, area, perimeter, or height of an isosceles triangle using any two known values. It supports multiple length and angle units for fast and accurate results.
My Request to All: If you enjoy using my Isosceles Triangle Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
Telegram Link – Join Our Telegram Channel
YouTube Link – Subscribe to Our YouTube Channel
For more tools, please visit our homepage at CalculationClub – Free Online Calculators
For additional tools in Hindi, you can visit MeterToFeet