Pythagorean Theorem Calculator
Right-angled triangle problems are common in math, physics, engineering, and even everyday tasks like measuring distances or constructing objects. But solving for unknown sides or angles can be tricky without the right tools. This is where the Pythagorean Theorem Calculator comes in.
Our Pythagorean Theorem Calculator is built to handle a wide range of right triangle calculations. It can solve for the missing side using the Pythagorean theorem and also compute related values such as Side, Area, Perimeter, Angles, and Height—all with step-by-step clarity and just a few clicks.
Let’s dive deeper into how this calculator works and how it can help you solve common right triangle problems with ease.
1. Basic Pythagorean Theorem Formula
The core formula of this calculator is the Pythagorean Theorem:
Formula:
$ c^2 = a^2 + b^2 $
This is used to find the length of the hypotenuse ($c$) when the lengths of the other two sides ($a$ and $b$) are known.
Example 1.1: Find the hypotenuse
What is the length of the hypotenuse if side $a = 3$ units and side $b = 4$ units?
$ c^2 = 3^2 + 4^2 $ $= 9 + 16 = 25 \Rightarrow c$ $= \sqrt{25} = 5 $
2. Finding a Missing Leg
When the hypotenuse and one leg are known, you can find the missing side using:
Formula:
$ a = \sqrt{c^2 – b^2} \quad$ or $\quad b = \sqrt{c^2 – a^2} $
Example 2.1: Find a missing leg
If the hypotenuse is $c = 13$ and one side is $a = 5$:
$ b^2 = 13^2 – 5^2 = 169 – 25$ $= 144 \Rightarrow b = \sqrt{144} = 12 $
3. Calculating Triangle Area
Once all sides are known, the area of the triangle can be calculated:
Formula:
$ \text{Area}$ = $\frac{1}{2} \times a \times b $
Example 3.1:
If $a = 6$ and $b = 8$:
$ \text{Area} = \frac{1}{2} \times 6 \times$ 8 = 24
4. Calculating Perimeter
The perimeter is the sum of all sides:
Formula:
$ \text{Perimeter} = a + b + c $
Example 4.1:
For sides $a = 5$, $b = 12$, and $c = 13$:
$ \text{Perimeter} = 5 + 12 + 13 = 30 $
5. Calculating Triangle Height
For a right triangle, the height with respect to the hypotenuse as base can be found using:
Formula:
$ \text{Height} = \frac{a \times b}{c} $
Example 5.1:
If $a = 6$, $b = 8$, and $c = 10$:
$ \text{Height} = \frac{6 \times 8}{10}$ = $\frac{48}{10} = 4.8 $
6. Finding Angles Using Trigonometry
You can also use basic trigonometric ratios:
$ \sin(\alpha) = \frac{\text{opposite}}{\text{hypotenuse}} $ = $\frac{\text{a}}{\text{c}} $
$ \cos(\beta) = \frac{\text{adjacent}}{\text{hypotenuse}} $ = $\frac{\text{b}}{\text{c}} $
$ \tan(\alpha) = \frac{\text{opposite}}{\text{adjacent}} $ = $\frac{\text{a}}{\text{b}} $
Example 6.1:
If $a = 3$, $b = 4$, and $c = 5$:
$ \sin(A) = \frac{3}{5} = 0.6$
$\Rightarrow A \approx \sin^{-1}(0.6) \approx 36.87^\circ $
$ \cos(A) = \frac{4}{5} = 0.8$
$ \Rightarrow B \approx \cos^{-1}(0.8) \approx 53.13^\circ $
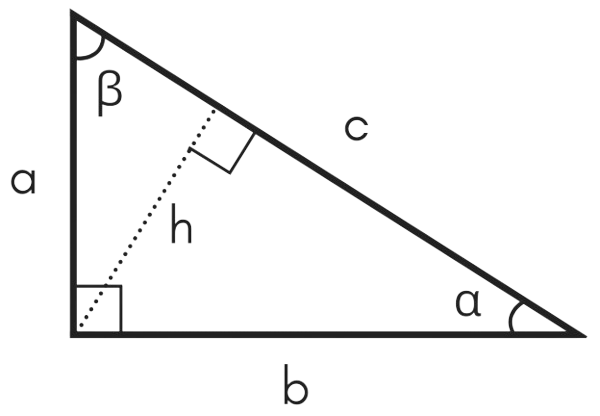
What is the Pythagorean Theorem?
The Pythagorean Theorem is a foundational concept in geometry that describes the relationship between the three sides of a right-angled triangle. It states:
$ c^2 = a^2 + b^2 $
Where:
$c$ is the hypotenuse (the side opposite the right angle)
$a$ and $b$ are the two other legs of the triangle
This formula only applies to right-angled triangles.
“The square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.”
This powerful theorem was first discovered and made famous by the Greek mathematician Pythagoras in the 6th century BC, and it remains one of the most widely used equations in mathematics today.
How to Manually Calculate Using the Pythagorean Theorem
1. Finding a Missing Leg
Use this when the hypotenuse ($c$) and one leg ($a$ or $b$) are known.
Formula:
$a = \sqrt{c^2 – b^2}$ or $b = \sqrt{c^2 – a^2}$Example 1:
If $c = 13$, $b = 5$
$a = \sqrt{13^2 – 5^2} = \sqrt{169 – 25} = \sqrt{144} = 12$Example 2:
If $c = 10$, $a = 6$
$b = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = \sqrt{64} = 8$
2. Calculating Triangle Area
Use the two legs ($a$ and $b$) of a right triangle.
Formula:
$\text{Area} = \dfrac{1}{2} \times a \times b$Example 1:
$a = 6$, $b = 8$
$\text{Area} = \dfrac{1}{2} \times 6 \times 8 = 24$Example 2:
$a = 5$, $b = 12$
$\text{Area} = \dfrac{1}{2} \times 5 \times 12 = 30$
3. Calculating Perimeter
Add up all three sides: $a$, $b$, and $c$.
Formula:
$\text{Perimeter} = a + b + c$Example 1:
$a = 3$, $b = 4$, $c = 5$
$\text{Perimeter} = 3 + 4 + 5 = 12$Example 2:
$a = 9$, $b = 12$, $c = 15$
$\text{Perimeter} = 9 + 12 + 15 = 36$
4. Calculating Triangle Height
Use this when area and base are known.
Formula:
$\text{Height} = \dfrac{2 \times \text{Area}}{\text{Base}}$Example 1:
Area = $30$, Base = $5$
$\text{Height} = \dfrac{2 \times 30}{5} = 12$Example 2:
Area = $42$, Base = $7$
$\text{Height} = \dfrac{2 \times 42}{7} = 12$
5. Finding Angles Using Trigonometry
Use the legs and hypotenuse with trigonometric functions.
Formulas:
$\sin(\theta) = \dfrac{a}{c}$ $\cos(\theta) = \dfrac{b}{c}$ $\tan(\theta) = \dfrac{a}{b}$Example 1:
$a = 3$, $b = 4$, $c = 5$
$\theta = \tan^{-1}\left(\dfrac{3}{4}\right) \approx 36.87^\circ$Example 2:
$a = 5$, $c = 13$
$\theta = \sin^{-1}\left(\dfrac{5}{13}\right) \approx 22.62^\circ$
How to Use the Online Pythagorean Theorem Calculator?
Follow these simple steps to solve right triangle problems quickly and accurately:
1. Select What to Solve For
Begin by choosing what you want to calculate from the dropdown menu:
Side a
Side b
Hypotenuse c
Area A
Each option uses the Pythagorean Theorem or related geometry formulas to compute the missing value based on your inputs.
2. Enter Known Values
Enter the required known side lengths depending on your selected option:
To solve for Side a, enter values for Side b and Hypotenuse c.
To solve for Side b, enter Side a and Hypotenuse c.
To solve for Hypotenuse c, enter both Side a and Side b.
To solve for Area A, enter values for both Side a and Side b.
You can also adjust:
Decimal Places: Choose how many decimal points you want in the result.
Units: Select from meters (m), centimeters (cm), millimeters (mm), yards (yd), feet (ft), or inches (in).
3. Click “Calculate”
Press the “Calculate” button. The calculator will instantly apply the appropriate formula and return the solution.
4. Show or Hide Steps
Click “Show Steps” to view a step-by-step breakdown of the formula used and the calculations involved.
Prefer a simple answer? Click “Hide Steps” to minimize the details.
5. Reset for a New Calculation
Use the “Reset” button to clear all fields and start a new calculation. This is helpful when solving multiple triangle problems back-to-back.
Pythagorean Theorem Calculator
Frequently Asked Questions (FAQs) on Pythagorean Theorem Calculator
1. What does the Pythagorean Theorem Calculator do?
This calculator helps you quickly find a missing side (leg or hypotenuse) of a right-angled triangle using the formula:
$c^2 = a^2 + b^2$.
It also computes triangle area, perimeter, and even height if enough information is provided.
2. When can I use the Pythagorean Theorem?
You can use it only for right-angled triangles—where one angle is exactly $90^\circ$.
3. How do I know which side is the hypotenuse?
The hypotenuse ($c$) is always the longest side and lies opposite the right angle. The other two sides are called legs ($a$ and $b$).
4. What if I only know one side?
You need at least two side lengths to use the Pythagorean Theorem. With just one side, the calculator cannot compute the rest.
5. Can the calculator find triangle area too?
Yes! If you provide the lengths of both legs ($a$ and $b$), it calculates the area using:
$\text{Area} = \dfrac{1}{2} \times a \times b$
6. Does this calculator show steps?
Yes, click “Show Steps” to view a detailed breakdown of the calculation process.
7. Can I change the units (like cm, ft, in)?
Absolutely. You can select from multiple units such as meters, centimeters, millimeters, feet, yards, or inches—and your result will match the chosen unit.
8. What if I enter invalid or incomplete values?
The calculator will prompt you to enter all the necessary numbers. If a field is empty or invalid, it won’t compute the result until corrected.
9. Is there any rounding option?
Yes, you can choose how many decimal places you want your result to be rounded to.
10. Is this calculator useful for trigonometry too?
Indirectly, yes. If you know two sides, you can manually apply trigonometric ratios like $\sin$, $\cos$, or $\tan$ to find the angles.
Final Thoughts: The Pythagorean Theorem Calculator is an essential tool for students, teachers, engineers, architects, and anyone working with right-angled triangles. Whether you’re solving for a missing side, checking if a triangle is right-angled, or calculating area and perimeter, this calculator ensures precision and efficiency.
By supporting multiple units, decimal rounding, and step-by-step solutions, it adapts to academic, professional, and practical use cases—making geometry simpler and more accessible for everyone.
My Request to All: If you enjoy using my Pythagorean Theorem Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
Telegram Link– Click Here
Youtube Link– Click Here
For more tools, please visit our homepage at Calculationclub.com.
For additional tools in Hindi, you can visit Meter to Feet
Thank you for your support!
