Scientific Calculator Online

Calculator
Powered by © CalculationClub

 

Scientific Calculator Online is an advanced tool for calculating everything from basic math to advanced functions like trigonometry, exponents, and logarithms. It even has constants like π and Euler’s number, along with factorial and gamma functions, among others.

Scientific Calculator Online

  1. This “Scientific Calculator Online” from CalculationClub helps simplify your calculations effortlessly.
  2. You can easily perform various mathematical operations, from basic arithmetic to advanced functions like trigonometry, logarithms, exponents, roots, factorials, and even gamma calculations.
  3. It’s important to understand all its functions to use our calculator effectively. Scroll below to learn how to use: the Scientific Calculator Online.

Scientific Calculator Online

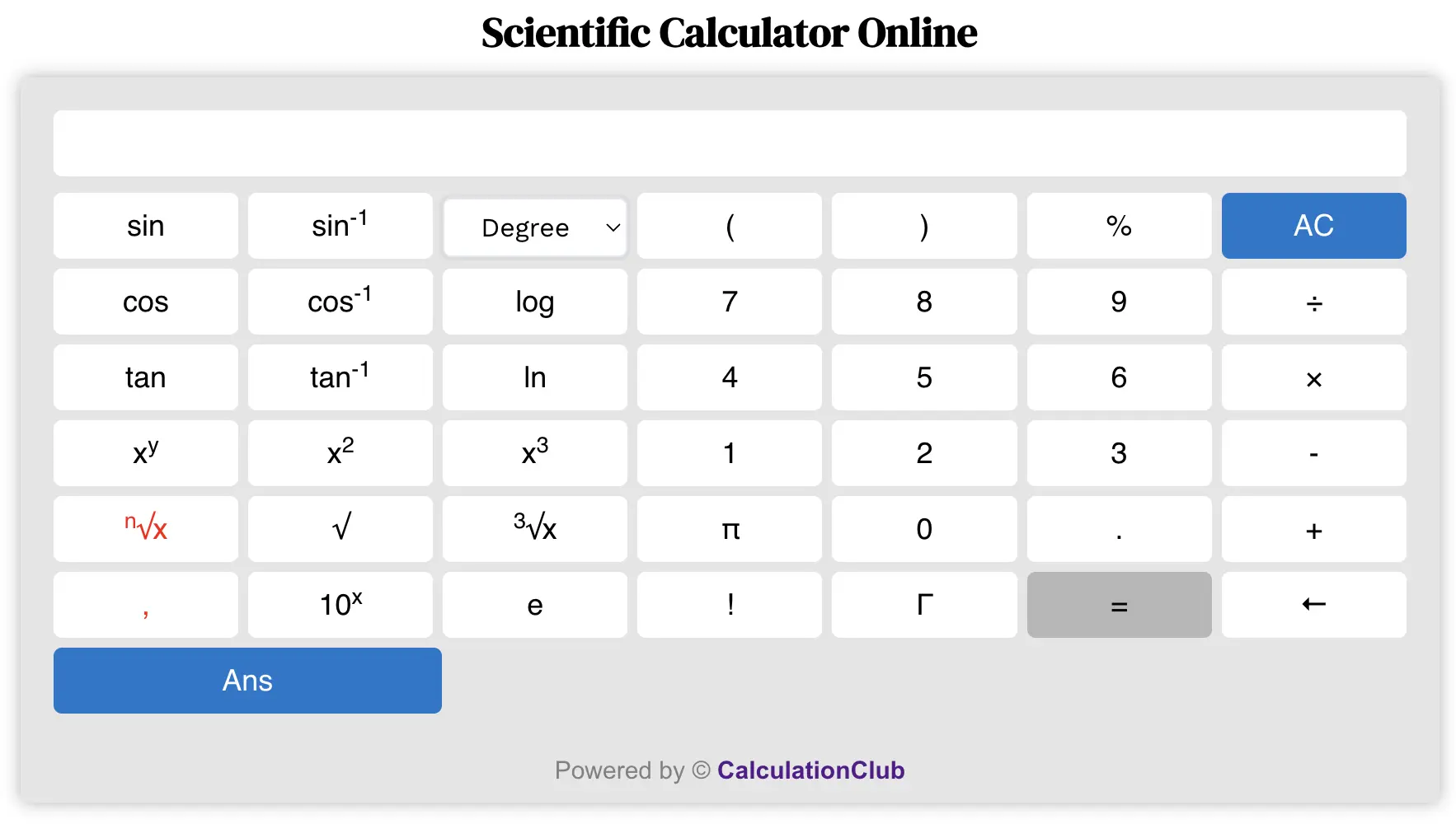
What Are the Functions of the Scientific Calculator Online?

Calculators are powerful tools that help us perform various mathematical calculations quickly and accurately. Whether it’s for simple arithmetic or complex scientific calculations, calculators provide a wide range of functions to meet our mathematical needs. In this blog post, we will explore the functions available on a Scientific Calculator Online and understand how they can be used.

Basic Arithmetic Operations

Let’s start with the basic arithmetic operations that every calculator offers:

  1. Addition (+)
  2. Subtraction (-)
  3. Multiplication (×)
  4. Division (÷)

Trigonometric Functions

  1. Sine (sin): This function calculates the sine of an angle. The user can input an angle in degrees or radians, and the calculator will return the corresponding sine value.
  2. Cosine (cos): This function calculates the cosine of an angle. Similar to the sine function, the user can input an angle in degrees or radians, and the calculator will return the corresponding cosine value.
  3. Tangent (tan): This function calculates the tangent of an angle. Once again, the user can input an angle in degrees or radians, and the calculator will return the corresponding tangent value.
  4. Arcsine (sin-1 or asin): The arcsine function, denoted as sin-1 or asin, calculates the angle (in degrees or radians) whose sine equals a given value. The input of arcsin(x) must be within the range of -1 to 1. The output of arcsin(x) is always between -π/2 and π/2 in radians. In terms of domain and range, arcsin(x) has a domain of [-1, 1] and a range of [-π/2, π/2]. This function is commonly used to find an angle when the sine value is known.
  5. Arccosine (cos-1 or acos): The arccosine function, denoted as cos-1 or acos, calculates the angle (in degrees or radians) whose cosine equals a given value. The input of arccos(x) must be within the range of -1 to 1. The output of arccos(x) is always between 0 and π in radians. In terms of domain and range, arccos(x) has a domain of [-1, 1] and a range of [0, π]. This function is commonly used to find an angle when the cosine value is known.
  6. Arctangent (tan-1 or atan): The arctangent function, denoted as tan-1 or atan, calculates the angle (in degrees or radians) whose tangent equals a given value. The input of arctan(x) can take any real number as it has a range of (-∞, ∞). The output of arctan(x) is always between -π/2 and π/2 in radians or -90° and 90° in degrees.

These trigonometric functions can be calculated in degrees or radians, depending on the mode selected by the calculator.

Exponential and Logarithmic Functions

Exponential and logarithmic functions are used in various mathematical and scientific calculations. Calculators often provide functions for these operations:

  1. Exponentiation (x^y) 
  2. Square (x^2) 
  3. Cube (x^3) 
  4. Square Root (√x) 
  5. Cube Root (3√x)
  6. nTh Root (n√x) 
  7. Natural Logarithm (ln): The natural logarithm function calculates the logarithm of a number to the base “e,” where “e” is the mathematical constant approximately equal to 2.71828.
  8. Common Logarithm (log): The common logarithm function calculates the logarithm of a number to the base 10.

Other Functions

In addition to the basic arithmetic, trigonometric, exponential, and logarithmic functions, calculators often provide several other useful functions. Here are a few examples:

  1. Percentage (%): The percentage function calculates a percentage of a given number.
  2. Pi (π): The pi function represents the mathematical constant π, which is approximately equal to 3.14159. It is widely used in geometry and trigonometry.
  3. Euler’s Number (e): Euler’s number, denoted by the letter “e,” is a mathematical constant approximately equal to 2.71828. It is often used in exponential and logarithmic calculations.
  4. Factorial (!): The factorial function calculates the product of all positive integers up to a given number.
  5. Gamma (Γ): The gamma function is a mathematical extension of the factorial function. It calculates the value of factorial for non-integer numbers. The gamma function is denoted by the Greek letter Γ.
  6. 10x: The 10x function raises 10 to a given power, useful for calculations involving powers of 10.

Additional Buttons on the Calculator

In addition to the functions we discussed earlier, online calculators often include several other buttons that serve specific purposes. Let’s explore these buttons:

  1. Clear History:  To clear the history, simply double-click the AC button. This action will clear the history, enabling you to begin anew with a fresh slate.
  2. AC (All Clear): The “AC” button performs an all-clear function. When pressed, it clears the display and any pending calculations, resetting the calculator to its initial state.
  3. Backspace (←): The backspace button, often represented by a left-pointing arrow (←), allows you to delete the last entered digit or character. It comes in handy when you make a mistake while entering a number or expression.
  4. Equals (=): The equals button (=) is used to perform the calculation and obtain the result. When pressed, it evaluates the entered expression and displays the calculated value on the screen.

How to Use Our Scientific Calculator Online?

Constants (π, e)
Pi (π) and Euler’s Number (e): The buttons labeled “π” and “e” represent the mathematical constants pi (π) and Euler’s number (e), respectively. You can use them in calculations just like any other number.
Addition (+)

To add two numbers, follow these steps:

  1. Enter the first number using the number buttons.
  2. Press the “+” button.
  3. Enter the second number using the number buttons.
  4. Press the “=” button to get the sum.
Example: 5+6=11

To add two numbers, one of which is negative, you can follow these steps:

  1. Enter the first number using the number buttons.
  2. Press the “+” button.
  3. Enter the second number with a negative sign enclosed in brackets, such as (-5).
  4. Press the “=” button to obtain the sum.

Example 1: Adding -5 and 6 Here’s how you can do it:

  1. Enter “-5” using the number buttons.
  2. Press the “+” button.
  3. Enter “6” using the number buttons.
  4. Press the “=” button to get the sum, which is “1”.
    • Result: -5 + 6 = 1.

Example 2: Adding 5 and -6 Here’s how you can do it:

  1. Enter “5” using the number buttons.
  2. Press the “+” button.
  3. Enter the number with a negative sign in brackets, like (-6).
  4. Press the “=” button to get the sum, which is “-1”.
    • Result: 5 + (-6) = -1.

If you want to add two functions such as sin, cos, tan, sin-1, cos-1, tan-1, log, ln, π, e, etc., you can follow these steps:

  1. Enter the first function using the corresponding button.
  2. Press the “+” button.
  3. Enter the second function using the appropriate button.
  4. Press the “=” button to get the sum.

 

Example: sin(30) + log(10) = 1.5

Note: It is important to ensure that you close any brackets where necessary, as failing to do so may result in a different answer.

Example: Let’s consider the expression sin(30+log(10).

Breaking down the steps:

  • ⇒ sin(30+log(10)
  • ⇒ sin(30+log(10), where log(10) equals 1
  • ⇒ sin(30+1)
  • ⇒ sin(31)
  • ⇒ sin(31) = 0.5150380749

⇒ It is important to ensure that you close brackets where necessary, as failing to do so may result in a different answer.

⇒ As demonstrated in this example, the calculator automatically applies the closed bracket to the expression. However, it is still essential to be mindful of closing brackets when working with complex calculations to ensure accurate results.

Subtraction (-)
To subtract two numbers or functions, you can follow the same steps as an addition but with a slight change in the sign.Example: 5 – 6 = -1
Example: 5 – (-6) = 11
Example: (-5) – 6 = -11
sin(30) – log(10) = -0.5
log(10) – sin(30)= 0.5
Multiplication (×)
To multiply two numbers or functions, you can follow the same steps as addition, but with a sign change.Example: 5 × 6 = 30
Example: 5 × (-6) = -30
Example: (-5) × 6 = -30
sin(30) × log(10) = 0.5 × 1= 0.5
log(10) × (-sin(30))= 1×(-0.5) = 0.5
 Division (÷)
To divide two numbers or functions, you can follow similar steps as mentioned for addition and multiplication, but with a sign changeExample: 30 ÷ 6 = 5
Example: 30 ÷ (-6) = -5
Example: (-30) ÷ 6 = -5
log(10) ÷ (-sin(30))= 1÷(-0.5) = -2
Percentage (%)

To calculate a percentage of a number, follow these steps:

  1. Enter the percentage value using the number buttons.
  2. Press the “%” button.
  3. Enter the number for which you want to find the percentage using the number buttons.
  4. Press the “=” button to get the result.

Example: Finding 20% of 80

  1. Enter “20” using the number buttons. [20  ]
  2. Press the “%” button.  [20%  ]
  3. Enter “80” using the number buttons. [20%×80  ]
  4. Press the “=” button to get the result [16]

The calculator will display “20% × 80” (the multiplication symbol is automatically applied) indicating that 20% of 80 is 16.

Trigonometric Functions (sin, cos, tan)

To use the trigonometric functions on the online calculator, follow these simplified steps:

  1. Select the mode: Choose whether you want to work with degrees or radians. Select either “Degree” or “Radian” based on your preference.
  2. Choose the trigonometric function you wish to use, such as sine (sin), cosine (cos), or tangent (tan).
  3. Enter the angle value: For example, if you want to find the sine of 30 degrees, enter “30” using the numerical buttons on the calculator.
  4. It is important to ensure that you close brackets where necessary, as failing to do so may result in a different answer.
  5. Press the “=” button to get the result.

By following these simplified steps, you can easily use the trigonometric functions on the online calculator to calculate values based on the entered angles in both degrees and radians.

Example: sin(30) where angle in degree.

  1. Select “Degree” mode.
  2. Press the “sin” button. [sin( ]
  3. Enter “30” using the number buttons. [sin(30 ]
  4. Close Bracket. [sin(30) ]
  5. Press the “=” button to get the result. [0.5]

Example: sin(30) where angle in radian.

  1. Select “Radian” mode.
  2. Press the “sin” button. [sin( ]
  3. Enter “30” using the number buttons. [sin(30 ]
  4. Close Bracket. [sin(30) ]
  5. Press the “=” button to get the result. [-0.9880316241]

Example: sin(X). where X is the group of all functions present on the calculator.
sin(5+log(10)+cos(60)+3^2+√(16)×e+π)= 0.4926471486
where X= 5+log(10)+cos(60)+3^2+√(16)×e+π = 29.5147199674 and brackets are properly closed.

In History Field
sinD(30) = 0.5, where D stands for the selected mode which is that degree.
sinR(30) = -0.9880316241, where R stands for the selected mode which is that Radian.
Trigonometric Functions (sin-1, cos-1, tan-1)

To use the trigonometric functions on the online calculator, follow these simplified steps:

  1. Select the mode: Choose whether you want the answer in degrees or radians. If you prefer degrees, select the degree mode. If you prefer radians, select the radian mode. Locate the mode selection option on the calculator interface and choose the desired mode.
  2. Choose the trigonometric function you wish to use, such as sin-1, cos-1, tan-1.
  3. Enter the value: For example, if you want to find the sin-1 of (0.5) {when mode is degrees}.
  4. It is important to ensure that you close brackets where necessary, as failing to do so may result in a different answer.
  5. Press the “=” button to get the result.

By following these simplified steps, you can easily use the trigonometric functions on the online calculator to calculate angles in both degrees and radians of different values.

Example: sin-1(0.5), we want to answer in degree.

  1. Select “Degree” mode.
  2. Press the “sin-1” button. [sin-1( ]
  3. Enter “0.5” using the number buttons. [sin-1(0.5 ]
  4. Close Bracket. [sin-1(0.5) ]
  5. Press the “=” button to get the result. [30]

Note:

  • The input of arcsin(x) must be within the range of -1 to 1.
  • The input of arccos(x) must be within the range of -1 to 1.
Logarithmic Functions (log, ln)

Logarithm (log): Use the “log” button to calculate the logarithm of a number. For example, to find the logarithm of 100, click the “log” button followed by the button labeled “100”.

Similarly, you can use the “ln” button to calculate the natural logarithm (base e) of a number. Just follow the same steps as above, but use the “ln” button instead of “log”.

Example: log(100)

  1. Press the “log” button. [log( ]
  2. Enter “100” using the number buttons. [log(100 ]
  3. Close Bracket. [log(100) ]
  4. Press the “=” button to get the result. [ 2 ]
Exponents

The online calculator offers functions for exponentiation, enabling you to perform calculations involving powers. Here’s a guide on how to use these operations:

Exponentiation (^): To raise a number to a power, follow these steps:

  1. Enter the base number using the number buttons.
  2. Click the “^” button to activate the exponentiation function.
  3. Press the exponent (power) using the number buttons.
  4. Press the “=” button to obtain the result.

Similarly These two buttons, “x²” and “x³,” on the online calculator function to calculate the square and cube of a number, respectively.

By following these steps, you can easily perform exponentiation calculations using the online calculator.

Example: Calculating 2 raised to the power of 3

  1. Enter “2” using the number buttons. [2]
  2. Click the “^” button. [2^]
  3. Press “3” using the number buttons. [2^3]
  4. Press the “=” button to calculate the result. [8]

Result: The calculator will display the value of 2 raised to the power of 3, which is 8.

Example: Calculating 2 raised to the power of -3.

  1. Enter “2” using the number buttons. [2]
  2. Click the “^” button. [2^]
  3. Press “(-3)” using the number buttons. [2^(-3)]
    • [2^(Y)] Please apply bracket if  Y= group of function or negative number.
  4. Press the “=” button to calculate the result. [0.125]

Result: The calculator will display the value of 2 raised to the power of -3, which is 0.125.

Root

Square Root (√)

  1. To calculate the square root of a number, use the square root (√) button.
  2. Press the “√” button.
  3. Enter the number or group of functions for which you want to calculate the square root using the number buttons.
  4. Closed the bracket
  5. Press the “=” button to obtain the Square Root result.

Example: √25

  1. Press the square root (√) button. [ √( ] 
  2. Enter “25”.   [ √(25 ] 
  3. Please Closed the bracket. [ √(25) ] 
  4. Press “=” to obtain the result.

Result: The calculator will display “5,” indicating the square root of 25 is 5.

Similarly: [ √(X) ], where x is a group of functions.

Cubic Root (√)

  1. To calculate the Cubic root of a number, use the Cubic root (∛) button.
  2. Press the “∛” button.
  3. Enter the number or group of functions for which you want to calculate the cubic root using the number buttons.
  4. Closed the bracket
  5. Press the “=” button to obtain the Cubic Root result.

Example: √25

  1. Press the square root (∛) button. [ ∛( ] 
  2. Enter “125”.   [ ∛(125 ] 
  3. Please Closed the bracket. [ ∛(125) ] 
  4. Press “=” to obtain the result.

Result: The calculator will display “5,” indicating the cubic root of 125 is 5.

Similarly: [ √(X) ], where x is a group of functions or negative number.

nth Root (n√x)

To calculate the nth Root of a number, use the [ n√x ] button. There are two ways to use it.

Method. 1 (If n is not a group of functions)

If n= Real Numbers (positive integers, negative integers, fractions, and decimals, but excluding imaginary numbers.) and X= Any number or Group of Functions.

  1. First, enter the value of n. If the number is negative, decimals use a bracket (-n), (3.4).
  2. Press the “n√x” button. But in display show “Root(“
  3. Enter the value of X in the form of a number or group of functions.
  4. Closed the bracket
  5. Press the “=” button to obtain the nth Root result.

 

Example.1: If we want a cubic root of 8. ( n=3 and x= 8)

  1. Enter the value of n=3. [ 3 ] 
  2. Press the “n√x” button.  [ 3Root( ] 
  3. Enter the value of x=8. [ 3Root(8 ] 
  4. Please Closed the bracket. [ 3Root(8) ] 
  5. Press “=” to obtain the result.

Result: The calculator will display “2,” indicating the cubic root of 8 is 2.

Example.2: If we want a cubic root of -8. ( n=3 and x= -8)

  1. Enter the value of n=3. [ 3 ] 
  2. Press the “n√x” button.  [ 3Root( ] 
  3. Enter the value of x=8. [ 3Root(-8 ] 
  4. Please Closed the bracket. [ 3Root(-8) ] 
  5. Press “=” to obtain the result.

Result: The calculator will display “-2,” indicating the cubic root of -8 is 2.

Example.2: If  (n=-3 and x= 8)

  1. Enter the value of ‘n’ in bracket=-3. [ (-3) ] 
  2. Press the “n√x” button.  [ (-3)Root( ] 
  3. Enter the value of x=8. [ (-3)Root(8 ] 
  4. Please Closed the bracket. [ (-3)Root(8) ] 
  5. Press “=” to obtain the result.

Result: The calculator will display “0.5”.

Similarly: [ n√(X) ], where x is a group of functions or negative number.

If n= Any number or Group of Functions. and X= Any number or Group of Functions.

  1. Press the “n√x” button. But in display show “Root(“
  2. Enter the value of n.
  3. Press the “,” button.
  4. Enter the value of X in the form of a number or group of functions.
  5. Closed the bracket
  6. Press the “=” button to obtain the nth Root result.

 

Example:

  1. Root(3,8) = 2
  2. Root(3,sin(30)+7.5) = 2
  3. Root(sin(30)+2.5,8) =2
  4. Root(3,-8) = -2
Factorials (!)

Online calculators provided by CalculationClub.com offer functionality to calculate factorials and the gamma function. Here’s how you can utilize these features:

Factorial (!): To calculate the factorial of a number, follow these steps:

  1. Press the “!” button.
  2. Enter the number or group of functions for which you want to calculate the factorial using the number buttons.
  3. Press the “=” button to obtain the factorial result.

Example: Calculating the factorial of 5

  1. Press the “!” button. [ factorial( ] 
  2. Enter “5” using the number buttons. [ factorial(5 ] 
  3. Please Closed the bracket. [ factorial(5) ] 
  4. Press the “=” button to calculate the factorial.

Result: The calculator will display “120,” which is the factorial of 5.

Similarly: [ factorial(X) ], where x is a group of functions.

Gamma (Γ)

Gamma (Γ) Function: To calculate the gamma function of a number, follow these steps:

  1. Press the “gamma” (Γ) button.
  2. Enter the number for which you want to calculate the gamma function using the number buttons.
  3. Press the “=” button to obtain the gamma function result.

Example: Calculating the gamma of 5

  1. Press the “Γ” button. [ gamma( ] 
  2. Enter “5” using the number buttons. [ gamma(5 ] 
  3. Please Closed the bracket. [ gamma(5) ] 
  4. Press the “=” button to calculate the factorial.

Result: The calculator will display “24,” which is the gamma of 5.

Similarly: [ gamma(X) ], where x is a group of functions.

Using Parentheses ” (, ) “
The online calculator allows you to use parentheses to group operations. Parentheses are a powerful tool in mathematical calculations as they allow you to group operations.
Memory Functions (Ans)
Memory Functions: The “Ans” button represents the previous answer, which can be used in subsequent calculations. Click the “Ans” button to recall the previous result.

Conclusion

In conclusion, the Scientific Calculator Online provides a versatile tool for performing calculations quickly and accurately. By following the step-by-step examples provided, you can easily input numbers and symbols, utilize operator buttons, and perform a variety of mathematical operations. Whether you need to perform simple math calculations, calculate percentages, or determine present or future values, the Online Calculator can assist you in achieving accurate results. Take advantage of the calculator’s functionality to enhance your productivity and streamline your mathematical calculations.

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top