Similar Triangles Calculator
The Similar Triangles Calculator is a free and easy-to-use online tool that helps you quickly find missing side lengths or verify proportional relationships between two similar triangles. Whether you know two sides of each triangle or a combination of sides and angles, simply enter the known values, and the calculator will instantly determine the missing dimensions with precision.
This tool is perfect for solving geometry problems that rely on triangle similarity rules, such as the AA (Angle-Angle), SSS (Side-Side-Side), or SAS (Side-Angle-Side) criteria. It’s especially useful for students, teachers, and professionals needing accurate calculations for real-world applications like design, surveying, architecture, or mathematics education.
The calculator also provides clear, step-by-step explanations of the similarity ratio and proportion method, making it ideal for learning geometric concepts, checking your work, or using as a quick reference—conveniently available anytime on CalculationClub.com.
How to Use the Online Similar Triangles Calculator
Whether you’re checking if two triangles are similar or calculating a missing side using triangle similarity rules, this free tool makes it quick and simple. Here’s how to use it:
1. Choose a Calculation Type
Select whether you want to:
- Check Similarity — Verify if two triangles are similar using one of the similarity criteria:
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- Find the Missing Side — Calculate an unknown side of one triangle based on its similarity to another.
2. Enter Known Values
Depending on the method selected, input the known side lengths or angles:
For example:
- For SSS, enter all three side lengths of both triangles.
- For SAS, enter two sides and the included angle.
- For ASA, input one side and two angles.
- To find a missing side, input the corresponding known sides from both triangles.
3. Set Decimal Precision and Units
Choose the number of decimal places (e.g., 3) for your results.
Select your unit of measurement from the list:
- Meters (m)
- Centimeters (cm)
- Millimeters (mm)
- Yards (yd)
- Feet (ft)
- Inches (in)
- Degrees (°) for angles
4. View Instant Results
Click the Calculate button to instantly get your results. The calculator will automatically apply the appropriate similarity rules to determine unknown values or confirm triangle similarity.
5. Show or Hide Calculation Steps
- Click “Show Steps” to see how the values were calculated using triangle similarity proportions. This is ideal for learning and verifying your work.
- Click “Hide Steps” for a cleaner summary display.
6. Reset for a New Calculation
Click the “Reset” button to clear all inputs and start a new comparison or calculation.
Similar Triangles Calculator
What is a Similar Triangles?
Similar triangles are two or more triangles that have the same shape, but not necessarily the same size. This means:
- All corresponding angles are equal.
- All corresponding side lengths are in the same ratio (proportional).
This proportionality preserves the triangle’s shape, even if one is larger or smaller than the other.
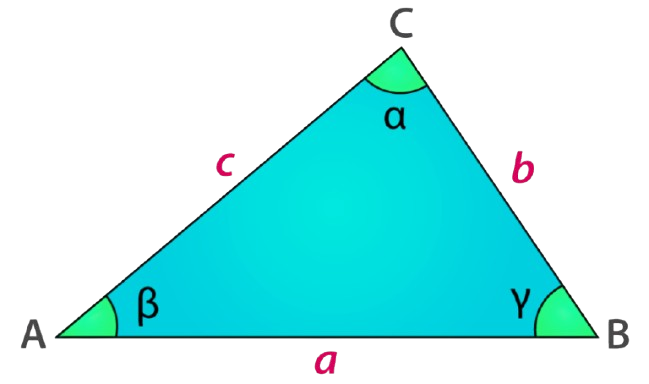 | 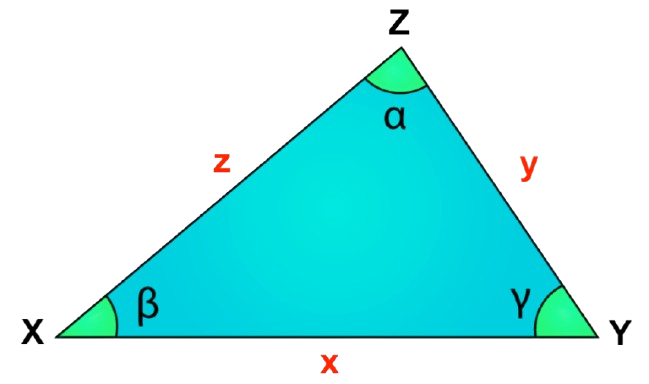 |
Two triangles, △ABC and △XYZ, are said to be similar, written as: △ABC ~ △XYZ
if:
- ∠A = ∠X
- ∠B = ∠Y
- ∠C = ∠Z
- AB / XY = BC / YZ = CA / ZX
This shows that angle measures match, and the sides are scaled versions of each other.
Properties of Similar Triangles:
- Corresponding Angles Are Equal:
∠A = ∠X, ∠B = ∠Y, ∠C = ∠Z - Corresponding Sides Are Proportional:
AB / XY = BC / YZ = AC / XZ - Same Shape, Different Size:
Similar triangles can be enlarged or reduced versions of each other. - Parallel Line Rule:
If a line is drawn parallel to one side of a triangle, it forms a new triangle that is similar to the original. - Area Ratio Rule:
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
If sides are in ratio a : b, then:
Area₁ / Area₂ = a² / b²
Criteria for Triangle Similarity
There are three standard similarity rules used to determine whether two triangles are similar:
1. AA (Angle-Angle) Similarity:
If two angles in one triangle are equal to two angles in another triangle, the triangles are similar. Since the sum of angles in a triangle is always 180°, knowing two angles is enough.
Example:
∠A = ∠X and ∠B = ∠Y ⟹ △ABC ~ △XYZ
2. SSS (Side-Side-Side) Similarity:
If the ratios of all three corresponding sides are equal, the triangles are similar.
Example:
If AB / XY = BC / YZ = AC / XZ, then △ABC ~ △XYZ
3. SAS (Side-Angle-Side) Similarity:
If two sides are in proportion and the included angle between them is equal, the triangles are similar.
Example:
If AB / XY = AC / XZ and ∠A = ∠X ⟹ △ABC ~ △XYZ
Example:
Let’s say you have:
Triangle 1:
- AB = 6 cm
- BC = 8 cm
- CA = 10 cm
Triangle 2:
- XY = 3 cm
- YZ = 4 cm
- ZX = 5 cm
The sides are in the ratio:
6:3 = 2
8:4 = 2
10:5 = 2
So, all corresponding sides are in a 2:1 ratio, and therefore:
△ABC ~ △XYZ
Summary of a Similar Triangles
- Angles- All corresponding angles are equal
- Sides- All corresponding sides are in proportion
- Shape- Always same
- Size- Can differ
- Symbols- △ABC ~ △XYZ
- Used in Architecture, surveying, navigation, modeling, etc.
Problem: SSS (Side-Side-Side) Similarity
Question.1:
Given the side lengths of two triangles:
Triangle ABC:
- AB = 3 meters
- BC = 4 meters
- CA = 5 meters
Triangle XYZ:
- XY = 6 meters
- YZ = 8 meters
- ZX = 10 meters
Determine whether the triangles are similar using the SSS Similarity Criterion, and if so, find the scale factor (k).
Solution: To use the SSS Similarity Rule, compare the ratios of corresponding sides.
$\frac{AB}{XY}$ = $\frac{3}{6}$ = 0.5
$\frac{BC}{YZ}$ = $\frac{4}{8}$ = 0.5
$\frac{CA}{ZX}$ = $\frac{5}{10}$ = 0.5
Since all three corresponding side ratios are equal, the triangles are similar by SSS Similarity.
Therefore: △ABC∼△XYZ
Scale Factor (k):
k = $\frac{AB}{XY}$ = $\frac{3}{6}$ = 0.5
Final Answer:
- Triangles ABC and XYZ are similar by SSS Similarity.
- The Scale Factor (k) is: k = $\frac{1}{2}$
Problem: SAS (Side-Angle-Side) Similarity
Question.2:
Given two triangles with the following measurements:
Triangle ABC:
- AB = 5 meters
- ∠B = 60°
- BC = 7.5 meters
Triangle XYZ:
- XY = 10 meters
- ∠Y = 60°
- YZ = 15 meters
Determine whether the triangles are similar using the SAS Similarity Criterion, and if so, find the scale factor (k).
Solution: To use the SAS Similarity Rule, compare the ratios of two sides and check if the included angles are equal.
∠B = ∠Y = 60°
$\frac{AB}{XY} = \frac{5}{10} = 0.5$
$\frac{BC}{YZ} = \frac{7.5}{15} = 0.5$
Since the included angles are equal and the side ratios are equal, the triangles are similar by SAS Similarity.
Therefore: △ABC ∼ △XYZ
Scale Factor (k):
k = $\frac{AB}{XY} = \frac{5}{10} = \frac{1}{2}$
Final Answer:
- Triangles ABC and XYZ are similar by SAS Similarity.
- The Scale Factor (k) is: k = $\frac{1}{2}$
Problem: AA (Angle-Angle) Similarity
Question.3:
Given the angles of two triangles:
Triangle ABC:
- ∠A = 45°
- ∠B = 60°
Triangle XYZ:
- ∠X = 45°
- ∠Y = 60°
Determine whether the triangles are similar using the AA Similarity Criterion.
Solution: To use the AA Similarity Rule, check if two corresponding angles are equal.
∠A = ∠X = 45°
∠B = ∠Y = 60°
Since two corresponding angles are equal, the triangles are similar by AA Similarity.
Therefore: △ABC ∼ △XYZ
Final Answer:
- Triangles ABC and XYZ are similar by AA Similarity.
- Since no sides are given, the scale factor is not determined, but shape similarity is confirmed.
Problem: Missing Side in Similar Triangles
Question.4:
Two triangles, △ABC and △DEF, are similar.
Given:
- AB = 6 cm
- BC = 9 cm
- AC = 12 cm
Triangle DEF:
- DE = 10 cm
- EF = 15 cm
- Find DF.
Using the property of similar triangles, corresponding sides are proportional. That is:
$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$
Solution: Use the ratios of the corresponding sides:
$\frac{AB}{DE} = \frac{6}{10} = 0.6$
$\frac{BC}{EF} = \frac{9}{15} = 0.6$
Since the ratios are equal, the triangles are similar by SSS Similarity.
Now, find DF using the ratio of corresponding sides:
$\frac{AC}{DF} = 0.6 \Rightarrow DF$ $= \frac{AC}{0.6} = \frac{12}{0.6} = 20$ cm
Final Answer:
- Triangles ABC and DEF are similar.
- The missing side DF = 20 cm
Frequently Asked Questions on Similar Triangle Calculator
1. What are similar triangles?
Similar triangles are triangles that have the same shape but may differ in size. This means their corresponding angles are equal, and their corresponding sides are in proportion (i.e., have the same ratio).
2. How does the similar triangle calculator work?
The calculator checks the similarity condition using various criteria like AA (Angle-Angle), SSS (Side-Side-Side), or SAS (Side-Angle-Side). Once similarity is confirmed, it calculates the scale factor and may also find unknown side lengths or angles.
3. What is the SSS Similarity Criterion?
SSS Similarity is used when all three sides of one triangle are proportional to the three sides of another triangle. If the ratios of corresponding sides are equal, the triangles are similar.
4. What is the AA Similarity Criterion?
AA (Angle-Angle) Similarity states that if two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.
5. Can I use any unit for the side lengths?
Yes, as long as you use the same unit for all sides in both triangles. The output will maintain the same unit throughout the result.
6. What is a scale factor in similar triangles?
The scale factor (k) is the ratio of the lengths of any two corresponding sides of similar triangles. It helps determine how much one triangle is scaled up or down compared to the other.
7. Can the calculator find missing side lengths?
Yes, if two triangles are known to be similar and enough information is provided, the calculator can determine missing sides or angles using proportionality rules.
8. What formulas are used by the calculator?
The main formulas used depend on the similarity criterion. For example:
- SSS: Check if $\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX}$
- SAS: Check if the included angle is equal and the two pairs of sides are proportional
- AA: Just confirm two matching angles
Once similarity is established, the calculator may use:
Missing side = known side × scale factor
Scale factor (k) = $\frac{\text{Side in Triangle 1}}{\text{Corresponding Side in Triangle 2}}$
9. Why are similar triangles important in geometry?
Similar triangles are used in geometry and real-world applications such as indirect measurement, surveying, map scaling, and architecture. They help determine distances and sizes when direct measurement is difficult or impossible.
10. Can I use this calculator for real-life problems?
Absolutely. You can apply it in any situation where you need to verify triangle similarity or find unknown side lengths using proportional relationships—for example, in construction, design, navigation, and trigonometry problems.
Final Thoughts: The Similar Triangle Calculator is a simple and reliable tool that helps you easily find missing sides or verify similarity between two triangles using known values. Whether you’re studying, teaching, or working professionally, it’s fast, accurate, and always ready for you on CalculationClub.com.
My Request to All: If you enjoy using my Similar Triangle Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
Telegram Link – Join Our Telegram Channel
YouTube Link – Subscribe to Our YouTube Channel
For more tools, please visit our homepage at CalculationClub – Free Online Calculators
For additional tools in Hindi, you can visit MeterToFeet
Thank you for your support!