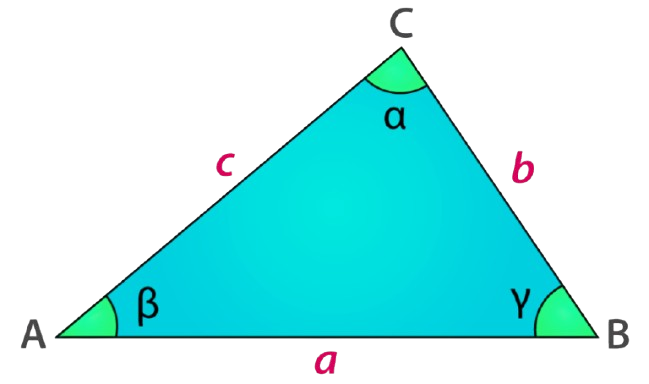
Triangle Calculator
The Triangle Calculator is a online tool designed to compute all key properties of a triangle based on your input—whether you provide all three sides (SSS), two sides and an included angle (SAS), two angles and one side (ASA or AAS), or two sides and a non-included angle (SSA).
It accurately calculates remaining angles (α, β, γ), sides (a, b, c), perimeter (P), semiperimeter (s), area (A) using Heron’s formula, heights (hₐ, hb, hc), medians (Mₐ, Mb, Mc), inradius (r), circumradius (R), diameter (D), circumference (C), circumcircle area (CA), and the area ratio (triangle to circumcircle). It also determines the type of triangle (scalene, isosceles, equilateral, or right-angled).
The Triangle Calculator is a handy all-in-one tool that combines the features of several triangle calculators into one. Instead of using separate tools, you can use this single calculator for tasks such as:
- Triangle Angle Calculator – to determine unknown interior angles based on given sides or angles
- Triangle Area Calculator – to calculate the area using Heron’s formula, base-height method, or trigonometric formulas
- Triangle Height Calculator – to compute the perpendicular altitudes from each vertex to the opposite side
- Triangle Median Calculator – to find the medians from each vertex to the midpoint of the opposite side
Triangle Angle Calculator
The Triangle Angle Calculator helps you accurately determine all the angles of a triangle. Whether you’re given all three sides, two sides and one angle, or two angles and one side, this tool provides a quick step-by-step solution to your problem.
Note: This calculator does not compute the third angle when only two angles are entered, as it is not designed for that. The third angle can be easily calculated by subtracting the sum of the two angles from 180° (or π radians).
In addition to calculating angles, this Triangle Angle Calculator also helps you find other unknown properties of your triangle, including: Perimeter (P), Semiperimeter (s), Area (A), Heights: ha, hb, hc, Medians: Ma, Mb, Mc, Inradius (r), Circumradius (R), Diameter (D), Circumference (C), Circumcircle Area (CA), Area Ratio (Circle : Triangle), Triangle Type.
Triangle Area Calculator
The Triangle Area Calculator helps you calculate the area of any triangle using different formulas — including Heron’s formula (when all three sides are known), the base-height formula (when height is known), or using trigonometry (when two sides and the included angle are given).
Triangle Height Calculator
The Triangle Height Calculator determines the perpendicular height (altitude) from a vertex to its opposite side. It provides accurate values for hₐ, hb, and hc — which are essential for calculating area using the base-height method.
Triangle Median Calculator
The Triangle Median Calculator computes the length of each median — the line segment from a vertex to the midpoint of the opposite side. Medians Mₐ, Mb, and Mc are useful for geometric analysis and constructions within a triangle.
What is a Triangle?
A triangle is a three-sided polygon formed by three straight line segments connected end to end. It has three sides, three angles, and three vertices. The sum of the interior angles of any triangle is always 180° (π radians). Triangles are classified based on their side lengths (scalene, isosceles, equilateral) and angles (acute, right, obtuse).
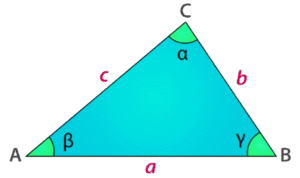
Note: In a triangle:
- Sides are the line segments between two vertices:
- AB (length a)
- BC (length b)
- CA (length c)
- Angles are formed at each vertex and lie opposite to their respective sides:
- ∠Alpha (α) is opposite side a, located at vertex C (between sides BC and CA)
- ∠Beta (β) is opposite side b, located at vertex A (between sides CA and AB)
- ∠Gamma (γ) is opposite side c, located at vertex B (between sides AB and BC)
- Vertices are the points where two sides meet:
- Vertex A: where sides CA and AB meet (∠α)
- Vertex B: where sides AB and BC meet (∠β)
- Vertex C: where sides BC and CA meet (∠γ)
Want to know what type of triangle you have? Use our
👉 Classifying Triangles Calculator — a free, user-friendly, and intelligent tool that helps you classify triangles based on side lengths, angle measures, or both.
Important Triangle Formulas
Below are some essential formulas commonly used to solve various triangle-related problems. These include basic formulas for perimeter and area, height and medians, as well as important trigonometric rules like the Law of Sines and the Law of Cosines. Together, these formulas help determine unknown sides, angles, and other properties of a triangle efficiently.
Before using the formulas, here are the standard notations and what they represent in a triangle:
- Side and Angle notations are already explained in the previous section.
- Perimeter: $P$ — The total length around the triangle (sum of all sides).
- Semiperimeter: $s$ — Half of the perimeter, used in formulas like Heron’s.
- Area: $A$ — The total surface enclosed within the triangle.
- Heights: $h_a$, $h_b$, $h_c$ — Perpendicular line segments (altitudes) drawn from the vertex opposite to sides $a$, $b$, and $c$, respectively.
- Medians: $M_a$, $M_b$, $M_c$ — Line segments drawn from the vertex opposite to sides $a$, $b$, and $c$, respectively, to the midpoint of those sides.
- Inradius: $r$ — Radius of the incircle (the circle inscribed inside the triangle).
- Circumradius: $R$ — Radius of the circumcircle (the circle passing through all three vertices).
- Diameter: $D$ — Diameter of the circumcircle, calculated as $D = 2R$.
- Circumference: $C$ — Circumference of the circumcircle, calculated as $C = 2\pi R$.
- Circumcircle Area: $C_A$ — Area of the circumcircle, calculated as $C_A = \pi R^2$.
1. Law of Cosines and Law of Sines
The Law of Cosines and the Law of Sines are essential tools in triangle geometry used to find unknown sides or angles when at least three values (such as two sides and one angle, or two angles and a side) are known. These formulas work for all triangles — not just right-angled ones — and are especially useful in solving non-right triangles.
i. Law of Cosines (Cosine Formula):
Used when you know two sides and the included angle (SAS) or all three sides (SSS) to find an angle.
$a^2 = b^2 + c^2 – 2bc \cdot \cos(\alpha)$
$b^2 = a^2 + c^2 – 2ac \cdot \cos(\beta)$
$c^2 = a^2 + b^2 – 2ab \cdot \cos(\gamma)$
Rearranged to find angles:
$\cos(\alpha) = \frac{b^2 + c^2 – a^2}{2bc}$
$\cos(\beta) = \frac{a^2 + c^2 – b^2}{2ac}$
$\cos(\gamma) = \frac{a^2 + b^2 – c^2}{2ab}$
ii. Law of Sines:
Used when you know two angles and a side (AAS or ASA), or two sides and a non-included angle (SSA).
$\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}$
a: b: c = Sin α: Sin β: Sin γ
3. Perimeter $P$
The perimeter of a triangle is the total length around the triangle — that is, the sum of the lengths of all its sides. It gives the total boundary measurement of the triangle.
$P = a + b + c$
4. Semiperimeter $s$
The semiperimeter of a triangle is half of its perimeter. It is commonly used in various triangle formulas, especially Heron’s formula for calculating area.
$s = \frac{a + b + c}{2}$
5. Area $A$
The area of a triangle is the amount of surface enclosed within its three sides. Depending on the known values (sides, base-height, or angle between sides), different formulas can be used to calculate the area.
i. Heron’s Formula (when all three sides are known):
$A = \sqrt{s(s – a)(s – b)(s – c)}$
Where s is the semiperimeter, calculated as:
$s = \frac{a + b + c}{2}$
ii. Using Base and Height (when height is known):
$A = \frac{1}{2} \times \text{base} \times \text{height}$
For example, if base = a and height = ha:
$A = \frac{1}{2} \times a \times h_a$
You can also use:
$A = \frac{1}{2} \times b \times h_b$
$A = \frac{1}{2} \times a \times h_c$
iii. Using Two Sides and the Included Angle:
$A = \frac{1}{2} \times a \times b \times \sin(γ)$
This method is used when two sides and the angle between them are known. You can also use:
$A = \frac{1}{2} \times b \times c \times \sin(α)$
$A = \frac{1}{2} \times c \times a \times \sin(β)$
6. Heights
Heights (also known as altitudes) of a triangle are the perpendicular line segments drawn from a vertex to the line containing the opposite side. Each height represents the shortest distance from a vertex to its corresponding base.
Specifically:
- $h_a$ is drawn from vertex C to side AB (a)
- $h_b$ is drawn from vertex A to side BC (b)
- $h_c$ is drawn from vertex B to side CA (c)
Heights are essential in calculating area using the base-height formula:
$A = \frac{1}{2} \times \text{base} \times \text{height}$
so, the area can be calculated using any of the following:
$A = \frac{1}{2} \times a \times h_a$
$A = \frac{1}{2} \times b \times h_b$
$A = \frac{1}{2} \times c \times h_c$
To rearrange the area formulas in terms of the heights $h_a$, $h_b$, and $h_c$, you solve each for the height:
$h_a = \frac{2A}{a}$
$h_b = \frac{2A}{b}$
$h_c = \frac{2A}{c}$
Each formula uses one side of the triangle as the base and the corresponding perpendicular height from the opposite vertex.
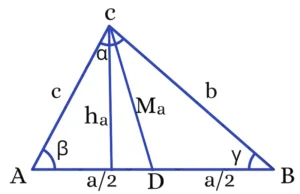
7. Medians
Medians of a triangle are the line segments drawn from each vertex to the midpoint of the opposite side. Each median divides the triangle into two smaller triangles of equal area.
Specifically:
- $M_a$ is drawn from vertex C to the midpoint of side AB (a)
- $M_b$ is drawn from vertex A to the midpoint of side BC (b)
- $M_c$ is drawn from vertex b to the midpoint of side CA (c)
Law of Cosines in Triangle ΔABC- This formula is used to find side b when two sides (a and c) and the included angle β are known:
$b^2 = a^2 + c^2 – 2ac \cdot \cos(\beta)$
Law of Cosines in Triangle ΔADC (for Median $M_a$)- If D is the midpoint of side AB, then triangle ΔADC is formed.
Using the Law of Cosines in triangle ΔADC, the formula for the median $M_a$ from vertex C to side AB becomes:
$M_a^2 = \left(\frac{a}{2}\right)^2 + c^2 – ac \cdot \cos(\beta)$
$M_a = \sqrt{ \left( \frac{a}{2} \right)^2 + c^2 – ac \cdot \cos(\beta) }$
similar
$M_b = \sqrt{ \left( \frac{b}{2} \right)^2 + a^2 – ab \cdot \cos(\gamma) }$
$M_c = \sqrt{ \left( \frac{c}{2} \right)^2 + b^2 – bc \cdot \cos(\alpha) }$
8. Inradius
The inradius (r) of a triangle is the radius of the incircle — a circle inscribed within the triangle, tangent to all three sides. It is directly related to the triangle’s area and semiperimeter.
$r = \frac{A}{s}$
Where: A = area of triangle, s = semi-perimeter = $\frac{a + b + c}{2}$
9. Circumradius
The circumradius (R) is the radius of the circumcircle — a circle that passes through all three vertices of the triangle.
$R = \frac{abc}{4A}$
This formula works for any triangle when all three sides and the area are known.
10. Circumcircle Diameter
The diameter (D) of the circumcircle is simply twice the circumradius:
$D = 2R = \frac{abc}{2A}$
11. Circumference of Circumcircle
The circumference is the total distance around the circumcircle.
$C = 2\pi R$
12. Circumcircle Area
The area of the circumcircle (Ac) is the surface enclosed by the circle passing through the triangle’s vertices.
$A_c = \pi R^2$
13. Area Ratio (Triangle to Circumcircle)
This ratio shows how much area the triangle occupies compared to its circumcircle:
$\text{Ratio} = \frac{A}{\pi R^2}$
Where R is the circumradius and A is the triangle’s area.
How to Use the Triangle Calculator
1. Enter Known Values: The Triangle Calculator features six main input fields — three for the sides (a, b, and c) and three for the angles (∠α, ∠β, and ∠γ). You can input any valid combination based on what values you already know.
You can enter:
- Three sides (SSS)
- Two sides and one included angle (SAS)
- Two angles and one side (ASA or AAS)
- Two sides and one non-included angle (SSA)
Note: If only two angles are provided, the third angle is not auto-computed in this calculator. You can manually find it as:
∠γ = 180° − (∠α + ∠β)
2. Choose Decimal Precision:
- Choose the number of decimal places (e.g., 2, 3, or more) for the output values.
- Select Units:
- Length Units: Meters (m), Centimeters (cm), Millimeters (mm), Yards (yd), Feet (ft), Inches (in)
- Angle Units: Degrees (°), Radians (rad)
3. Click “Calculate”: Once you’ve entered the required inputs, press the Calculate button. It accurately calculates remaining angles (α, β, γ), sides (a, b, c), perimeter (P), semiperimeter (s), area (A) using Heron’s formula, heights (hₐ, hb, hc), medians (Mₐ, Mb, Mc), inradius (r), circumradius (R), diameter (D), circumference (C), circumcircle area (CA), and the area ratio (triangle to circumcircle). It also determines the type of triangle (scalene, isosceles, equilateral, or right-angled).
4. Show/Hide Steps: Toggle the “Show Steps” option if you want to see detailed calculation steps or hide them for a cleaner view.
5. Reset: Use the Reset button to clear all inputs and start a fresh calculation.
Triangle Calculator
Frequently Asked Questions (FAQs) on Triangle Calculator
1. What is the Triangle Calculator used for?
The Triangle Calculator is an all-in-one tool designed to compute every important property of a triangle—such as angles, sides, perimeter, area, heights, medians, inradius, circumradius, and more—based on the values you input.
2. What triangle inputs can I provide?
You can enter any of the following:
- Three sides (SSS)
- Two sides and an included angle (SAS)
- Two angles and one side (ASA or AAS)
- Two sides and a non-included angle (SSA)
3. Can it find triangle height or medians?
Absolutely. It functions as a Triangle Height Calculator and a Triangle Median Calculator, calculating perpendicular altitudes (ha, hb, hc) and medians (Ma, Mb, Mc) from each vertex.
4. Does it work for any triangle type?
Yes. It supports all triangle types—scalene, isosceles, equilateral, and right-angled triangles.
5. Can I choose units for the inputs and outputs?
Yes. You can select from various units for both lengths (m, cm, mm, ft, in, yd) and angles (degrees, radians).
6. Will it show calculation steps?
Yes. You can enable the “Show Steps” option to see detailed step-by-step calculations.
7. Is the third angle auto-calculated if I enter only two angles?
No. If you enter only two angles, the calculator will not auto-compute the third. However, you can easily find it using:
∠γ = 180° − (∠α + ∠β)
Final Thoughts: The Triangle Calculator is an all-in-one tool that quickly computes all key properties of any triangle — including sides, angles, area, perimeter, height, medians, inradius, and circumradius — using any valid combination of inputs such as SSS, SAS, ASA, AAS, or SSA. It supports a wide range of length and angle units, offers precise results, and even classifies the triangle type (scalene, isosceles, equilateral, or right-angled), making it ideal for fast, detailed geometric analysis.
My Request to All: If you enjoy using my Triangle Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
For more tools, please visit our homepage at Calculationclub.com.
For additional tools in Hindi, you can visit Meter to Feet
Thank you for your support!
