Circumscribed Circle Calculator
A Circumscribed Circle Calculator is a online calculator which helps to compute important geometrical properties of a triangle and its corresponding circumcircle—a circle that passes through all three vertices of the triangle. By inputting the lengths of the three sides of a triangle, this calculator helps determine several key values: Triangle Perimeter, Triangle Area, Inradius, Circumradius, Circumcircle Diameter, Circumference, Circumcircle Area, Area Ratio (Circle : Triangle)
No matter if you’re a student, educator, or professional, this calculator delivers instant, precise results with clear, step-by-step calculations—removing the guesswork and deepening your understanding of triangle geometry.
How to Use the Circumscribed Circle Calculator
The Circumscribed Circle Calculator helps you find key properties of a triangle and its circumcircle using the lengths of all three sides. It calculates values like perimeter, area, inradius, circumradius, diameter, and more—along with optional step-by-step solutions.
1. Enter the lengths of the triangle’s sides (a, b, and c): Input the side values in meters (e.g., a = 7, b = 8, c = 9) into the corresponding fields.
2. Choose the decimal precision: Set how many decimal places you want the results to display. The default is 3, but you can increase or decrease this for more or less detail.
3. Select the unit of measurement: Ensure “meter” is selected for side lengths and “degree” for any angle-based values, maintaining consistency in the results.
4. Click the “Calculate” button: The calculator will instantly generate all the key values, such as perimeter, area, inradius, circumradius, circumference, and the area of the circumcircle.
5. Click “Show Steps” if needed: To understand how each result is derived, you can enable step-by-step calculations for a deeper learning experience.
6. Use “Reset” to clear and start over: If you want to calculate a new triangle, just click the Reset button to clear all fields without refreshing the page.

Circumscribed Circle Calculator
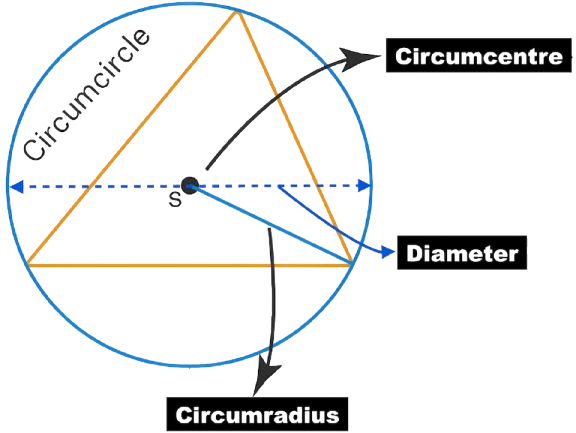
Circumscribed Circle?
A circumscribed circle (also known as a circumcircle) is the unique circle that passes through all the vertices of a polygon, most commonly a triangle. Here’s a breakdown of what it means:
A circumscribed circle is a circle drawn around a polygon such that:
- All the vertices (corners) of the polygon lie exactly on the circumference of the circle.
- The center of this circle is called the circumcenter.
- The radius is called the circumradius.
Circumcircle of a Triangle:
For any triangle (acute, right, or obtuse), a unique circumcircle can always be constructed.
- Circumcenter: The point where the perpendicular bisectors of the triangle’s sides intersect.
- Position of Circumcenter:
- Inside the triangle (acute triangle)
- On the hypotenuse (right triangle)
- Outside the triangle (obtuse triangle)
Definition of Geometric Terms Related to Triangles and Circles
1. Perimeter
The perimeter is the total length around a figure. For a triangle, it is the sum of the lengths of its three sides.
Perimeter = a + b + c
Example: If a triangle has sides \( a = 5 \), \( b = 6 \), and \( c = 7 \), then
Perimeter = 5 + 6 + 7 = 18 units
2. Area
The area is the measure of space enclosed by a triangle.
Using base and height:
\[\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}\]
Using Heron’s Formula:
$s = \frac{a + b + c}{2}$
$\text{Area} = \sqrt{s(s – a)(s – b)(s – c)}$
3. Inradius
The inradius is the radius of the largest circle that fits inside the triangle and touches all three sides (incircle).
\[r = \frac{A}{s}\]
Where \( A \) is the area of the triangle and \( s \) is the semi-perimeter.
4. Circumradius
The circumradius is the radius of the circle that passes through all three vertices of the triangle (circumcircle).
\[R = \frac{abc}{4A}\]
Where \( a \), \( b \), \( c \) are the side lengths and \( A \) is the area.
5. Diameter
The diameter is the longest straight-line distance through the center of a circle.
\[\text{Diameter} = 2R\]
Where \( R \) is the radius (or circumradius in the case of a triangle’s circumcircle).
6. Circumference
The circumference is the perimeter of a circle.
$\text{Circumference} = 2\pi R$
Where \( R \) is the radius of the circle.
7. Circumcircle Area
The area of the circumcircle that passes through all the vertices of a triangle.
\[\text{Circumcircle Area} = \pi R^2\]
Where \( R \) is the circumradius.
8. Area Ratio (Circle : Triangle)
This is the ratio of the area of the circumcircle to the area of the triangle.
\[\text{Ratio} = \frac{\pi R^2}{A}\]
Where \( R \) is the circumradius and \( A \) is the triangle’s area.
Example: Find Perimeter, Area, Inradius, Circumradius, Diameter, Circumference, Circumcircle Area, and Area Ratio for a triangle with sides $a = 5$, $b = 5$, $c = 8$.
Given:
Side lengths: $a = 5$, $b = 5$, $c = 8$ units.
No angles are given.
Check Triangle Validity (Triangle Inequality Theorem)
$5 + 5 = 10 > 8 \quad \checkmark$
$5 + 8 = 13 > 5 \quad \checkmark$
$8 + 5 = 13 > 5 \quad \checkmark$
All inequalities are satisfied, so the triangle is valid.
Calculate the Perimeter
$P = a + b + c = 5 + 5 + 8 = 18$ units
Calculate the Semi-perimeter
$s = \frac{P}{2} = \frac{18}{2} = 9$
Calculate the Area using Heron’s formula
$A = \sqrt{s(s – a)(s – b)(s – c)} =$$ \sqrt{9(9-5)(9-5)(9-8)} =$$ \sqrt{9 \times 4 \times 4 \times 1} =$$ \sqrt{144} = 12$ square units
Calculate the Inradius
$r = \frac{A}{s} = \frac{12}{9} = $$\frac{4}{3} \approx 1.33$ units
Calculate the Circumradius
$R = \frac{abc}{4A} =$$ \frac{5 \times 5 \times 8}{4 \times 12} =$$ \frac{200}{48} = \frac{25}{6} \approx 4.17$ units
Calculate the Diameter of the Circumcircle
$D = 2R = 2 \times 4.17 =$$ 8.33$ units
Calculate the Circumference of the Circumcircle
$C = 2 \pi R =$$ 2 \pi \times 4.17 \approx 26.18$ units
Calculate the Area of the Circumcircle
$A_{\text{circle}} = \pi R^2 =$$ \pi \times (4.17)^2 \approx 54.58$ square units
Calculate the Area Ratio (Circle : Triangle)
$\text{Area Ratio} = \frac{A_{\text{circle}}}{A} =$$ \frac{54.58}{12} \approx 4.55$
Frequently Asked Questions (FAQs) on Circumscribed Circle Calculator
1. What is a Circumscribed Circle Calculator?
A Circumscribed Circle Calculator is an online or software tool that computes the circumradius and other related properties of a triangle or polygon based on the input of side lengths or coordinates of vertices. It helps find the radius and center of the circle passing through all vertices.
2. What inputs are needed for the calculator?
Typically, you need to input: The lengths of the three sides of a triangle.
3. What outputs does the calculator provide?
Most calculators provide:
- The circumradius (radius of the circumscribed circle)
- The circumcenter (coordinates of the circle’s center) if coordinate inputs are given
- The diameter of the circumcircle
- Sometimes additional values like the area of the circumcircle or perimeter (circumference) of the circumcircle.
4. Can this calculator be used for polygons other than triangles?
While primarily designed for triangles, some advanced calculators can handle cyclic polygons (polygons that have a circumscribed circle). However, for general polygons, circumscribed circles may not exist.
5. How is the circumradius calculated?
For a triangle with sides a,b,c and area A, the circumradius R is calculated by the formula:
𝑅 = $ \frac{abc}{4A}$
6. Why is the circumcircle important in geometry?
The circumcircle helps in many geometric constructions and proofs. It also aids in understanding relationships between points, angles, and lengths in triangles and cyclic polygons.
7. What if the inputs do not form a valid triangle?
The calculator will typically give an error or notify that the inputs cannot form a triangle. For example, if the sum of any two sides is less than or equal to the third side, no triangle (and thus no circumcircle) exists.
Final Thoughts: The Circumscribed Circle Calculator is a quick and reliable tool that helps students, teachers, and professionals compute key properties of a triangle and its circumcircle. By simply entering side lengths, users get instant and accurate results for values like perimeter, area, inradius, circumradius, and more—making it an essential resource for anyone studying or applying geometric principles.
My Request to All: If you enjoy using my Circumscribed Circle Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
Telegram Link – Join Our Telegram Channel
YouTube Link – Subscribe to Our YouTube Channel
For more tools, please visit our homepage at CalculationClub – Free Online Calculators
For additional tools in Hindi, you can visit MeterToFeet
Thank you for your support!