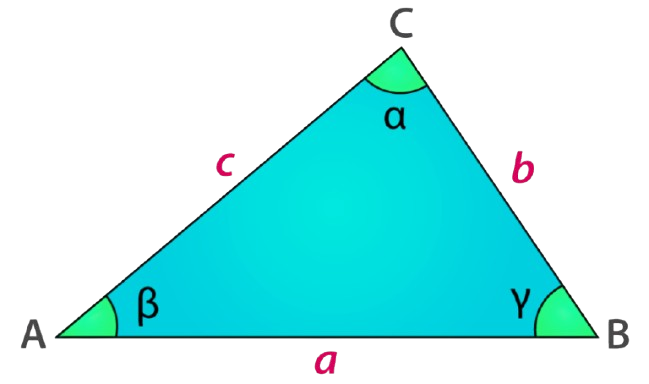
Heron’s Formula Calculator
A Heron’s Formula Calculator is an online calculator which help to calculate fundamental triangle properties using just three known quantities among side lengths, perimeter, and area. Whether you’re solving for an unknown side, computing the triangle’s area, or determining the perimeter, this calculator uses the power of Heron’s Formula to fill in the blanks with accuracy and ease.
By inputting any three values—such as two sides and the area, or the perimeter and one side—this calculator instantly solves for the remaining values by rearranging Heron’s formula and leveraging geometric identities. It delivers the following results: Side Lengths (a, b, c), Triangle Perimeter, and Triangle Area, depending on which three inputs are provided.
No matter if you’re a student tackling geometry problems, an educator demonstrating triangle theory, or a designer verifying structural measurements, this tool offers instant and accurate results, complete with step-by-step breakdowns—empowering deeper insight into triangle properties through Heron’s formula.
How to Use the Heron’s Formula Calculator
The Heron’s Formula Calculator is a smart tool that lets you determine unknown triangle properties—such as side lengths, area, or perimeter—by entering any three known values. It uses the powerful Heron’s formula to find missing quantities and provides accurate results instantly, including optional step-by-step solutions.
1. Enter any 3 values among sides (a, b, c), perimeter, or area: You can input any combination of known values. For example, enter sides a = 2 m, b = 3 m, and area = 2.9 m² to calculate the remaining side and perimeter.
2. Choose the decimal precision: Set how many decimal places you’d like to see in the output. The default is 3 decimal places, but you can modify this based on your needs.
3. Select the units of measurement: Use “meter” for length inputs and “degree” where applicable. Consistent units ensure accurate and meaningful results.
4. Click the “Calculate” button: The calculator will instantly compute all possible values, including the third side (if missing), the triangle’s perimeter, and the area using Heron’s formula.
5. Click “Show Steps” if desired: For educational purposes or curiosity, you can view the detailed breakdown of Heron’s formula used in your calculations.
6. Use “Reset” to start fresh: To calculate a new triangle, just click the Reset button to clear all inputs without reloading the page.

Heron’s Formula Calculator
What is Heron’s Formula?
Heron’s Formula is a powerful method to calculate the area of a triangle when the lengths of all three sides are known. It eliminates the need to know the height of the triangle and is especially useful for non-right-angled triangles.
Heron’s Formula calculates the area using:
- The lengths of the three sides: a, b, and c.
- The semi-perimeter (half the triangle’s perimeter).
- A square root expression involving all three sides and the semi-perimeter.
Formula for Area Using Heron’s Method:
- Semi-Perimeter (s):
$s = \frac{a + b + c}{2}$
- Area:
$Area = \sqrt{s(s – a)(s – b)(s – c)}$
1. Perimeter
The perimeter is the total length around the triangle—sum of the three side lengths.
Perimeter = a + b + c
Example: If a triangle has sides a = 5, b = 6, and c = 7,
Perimeter = 5 + 6 + 7 = 18 units
2. Area
The area is the total space enclosed within the triangle.
Using base and height:
$Area = \frac{1}{2} × base × height$
Using Heron’s Formula (when height is unknown):
$s = \frac{a + b + c}{2}$
$Area = \sqrt{s(s – a)(s – b)(s – c)}$
How to Find the Third Side Given Two Sides and the Area?
If you know two sides of a triangle and the area, you can calculate the third side using two different methods depending on the available information. The process involves either working backwards through Heron’s formula or using the sine area rule and the law of cosines.
Method 1: Using Heron’s Formula (When Only Area and Two Sides are Known)
Given: Side a, side b, and area A.
Let the unknown third side be c. First, define the semi-perimeter:
s = (a + b + c) / 2
Now apply Heron’s formula for area:
A = √[s(s − a)(s − b)(s − c)]
To solve for c:
- Square both sides of the equation.
- Substitute the known values of
a,b, andA. - You’ll get a non-linear equation in terms of
c, which may need to be solved numerically or using a calculator.
Note: This method is mathematically intensive and best handled by a computer-based equation solver or a triangle calculator with side-solver functionality.
Method 2: Using Trigonometry (If Angle Between Sides is Known or Can Be Estimated)
If the angle C between the two known sides (a and b) is known, use the sine area formula:
A = ½ × a × b × sin(C)
Rearranging to find angle C:
sin(C) = (2 × A) / (a × b)
Then compute angle C using inverse sine:
C = sin-1[(2A) / (ab)]
Once angle C is known, apply the Law of Cosines to find the third side c:
c² = [a² + b² − 2ab × cos(C)]
c² = √[a² + b² − 2ab × cos(C)]
Example:
Given: a = 6 units, b = 8 units, A = 18 square units
- Step 1: sin(C) = (2 × 18) / (6 × 8) = 0.75
- Step 2: C = sin-1(0.75) ≈ 48.59°
- Step 3: c = √[6² + 8² − 2 × 6 × 8 × cos(48.59°)] ≈ 6.92 units
Conclusion: The third side is approximately 6.92 units.
Calculate the Triangle’s Perimeter, Semiperimeter, and Area Using Heron’s Formula
Given:
- Side \( a = 3 \, \text{meters} \)
- Side \( b = 4 \, \text{meters} \)
- Side \( c = 5 \, \text{meters} \)
Step 1: Calculate the Perimeter \( P \)
\[ P = a + b + c = 3 + 4 + 5 = 12 \, \text{meters} \]
Step 2: Calculate the Semiperimeter \( s \)
\[ s = \frac{a+b+c}{2} = \frac{12}{2} = 6 \, \text{meters} \]
Step 3: Calculate the Area \( A \) using Heron’s Formula
Heron’s Formula:
\[ A = \sqrt{s(s-a)(s-b)(s-c)} \]
Substitute the known values:
\[ A = \sqrt{6 \times (6-3) \times (6-4) \times (6-5)} \]
Simplify the expression:
\[ A = \sqrt{6 \times 3 \times 2 \times 1} = \sqrt{36} = 6 \, \text{m}^2 \]
✅ Final Answer:
- Perimeter \( P = 12 \, \text{meters} \)
- Semiperimeter \( s = 6 \, \text{meters} \)
- Area \( A = 6 \, \text{m}^2 \)
Find the Unknown Sides of a Triangle Given Area and Perimeter
Given:
- Side \( c = 5 \, \text{meters} \)
- Area \( A = 6 \, \text{m}^2 \)
- Perimeter \( P = 12 \, \text{meters} \)
Step 1: Use Perimeter Formula to Express Side a in Terms of b
\[ P = a + b + c \Rightarrow a = P – b – c \]
Substitute known values: \( a = 12 – b – 5 = 7 – b \)
Step 2: Use Heron’s Formula to Find Valid Sides a and b
\[ s = \frac{a + b + c}{2} = \frac{12}{2} = 6 \]
\[ A = \sqrt{s(s – a)(s – b)(s – c)} \]
Substitute known values and \( a = 7 – b \):
\[ 6 = \sqrt{6(6 – (7 – b))(6 – b)(6 – 5)} \]
Simplifies to:
\[ 6 = \sqrt{6(b – 1)(6 – b)(1)} \Rightarrow 36 = 6(b – 1)(6 – b) \]
Divide both sides by 6:
\[ 6 = (b – 1)(6 – b) \]
Step 3: Solve the Quadratic Equation
Expanding: \( (b – 1)(6 – b) = -b^2 + 7b – 6 \)
Set equal to 6:
\[ -b^2 + 7b – 6 = 6 \Rightarrow b^2 – 7b + 12 = 0 \]
Solving: \( (b – 3)(b – 4) = 0 \Rightarrow b = 3 \text{ or } 4 \)
Step 4: Substitute Back to Find a
If \( b = 4 \Rightarrow a = 7 – 4 = 3 \)
Or \( b = 3 \Rightarrow a = 7 – 3 = 4 \)
So the triangle sides are: \( a = 3, b = 4, c = 5 \)
Step 5: Confirm Semiperimeter and Area
Check: \( s = \frac{3 + 4 + 5}{2} = 6 \)
Area = \( \sqrt{6(6 – 3)(6 – 4)(6 – 5)} = \sqrt{6 \cdot 3 \cdot 2 \cdot 1} = \sqrt{36} = 6 \)
Final Answer:
- Side a = 3 meters
- Side b = 4 meters
- Side c = 5 meters
- Area = 6 m²
- Perimeter = 12 meters
Calculate Missing Side and Area Using Heron’s Formula
Given:
- Side \( a = 3 \, \text{meters} \)
- Side \( b = 4 \, \text{meters} \)
- Perimeter \( P = 12 \, \text{meters} \)
Step 1: Calculate Side \( c \)
\[ c = P – a – b = 12 – 3 – 4 = 5 \, \text{meters} \]
Step 2: Calculate the Semiperimeter \( s \)
\[ s = \frac{a + b + c}{2} = \frac{3 + 4 + 5}{2} = \frac{12}{2} = 6 \, \text{meters} \]
Step 3: Calculate the Area \( A \) Using Heron’s Formula
Heron’s Formula:
\[ A = \sqrt{s(s – a)(s – b)(s – c)} \]
Substitute known values:
\[ A = \sqrt{6 \times (6 – 3) \times (6 – 4) \times (6 – 5)} \]
Simplify:
\[ A = \sqrt{6 \times 3 \times 2 \times 1} = \sqrt{36} = 6 \, \text{m}^2 \]
✅ Final Answer:
- Side \( c = 5 \, \text{meters} \)
- Semiperimeter \( s = 6 \, \text{meters} \)
- Area \( A = 6 \, \text{m}^2 \)
Calculate Third Side and Verify Area Using Trigonometry and Heron’s Formula
Given:
- Side \( a = 3 \, \text{meters} \)
- Side \( b = 4 \, \text{meters} \)
- Area \( A = 6 \, \text{m}^2 \)
Step 1: Use the Area Formula to Find Angle \( \theta \)
Area Formula:
\[ A = \frac{1}{2} ab \sin(\theta) \]
Rearranging to find \( \sin(\theta) \):
\[ \sin(\theta) = \frac{2A}{ab} = \frac{2 \times 6}{3 \times 4} = \frac{12}{12} = 1 \]
Therefore:
\[ \theta = \sin^{-1}(1) = 90^\circ \]
Step 2: Use the Law of Cosines to Find Side \( c \)
\[ c^2 = a^2 + b^2 – 2ab\cos(\theta) \]
Substitute values:
\[ c^2 = 3^2 + 4^2 – 2 \cdot 3 \cdot 4 \cdot \cos(90^\circ) \]
Since \( \cos(90^\circ) = 0 \):
\[ c^2 = 9 + 16 – 0 = 25 \Rightarrow c = \sqrt{25} = 5 \, \text{meters} \]
Step 3: Calculate the Perimeter \( P \)
\[ P = a + b + c = 3 + 4 + 5 = 12 \, \text{meters} \]
Step 4: Calculate the Semiperimeter \( s \)
\[ s = \frac{a + b + c}{2} = \frac{12}{2} = 6 \, \text{meters} \]
Step 5: Verify Area Using Heron’s Formula
Heron’s Formula:
\[ A = \sqrt{s(s – a)(s – b)(s – c)} \]
Substitute known values:
\[ A = \sqrt{6(6 – 3)(6 – 4)(6 – 5)} \]
Simplify:
\[ A = \sqrt{6 \cdot 3 \cdot 2 \cdot 1} = \sqrt{36} = 6 \, \text{m}^2 \]
✅ Final Answer:
- Angle \( \theta = 90^\circ \)
- Side \( c = 5 \, \text{meters} \)
- Perimeter \( P = 12 \, \text{meters} \)
- Semiperimeter \( s = 6 \, \text{meters} \)
- Area Verified \( A = 6 \, \text{m}^2 \)
Frequently Asked Questions (FAQs) on Heron’s Formula Calculator
1. What is Heron’s Formula?
Heron’s Formula is a mathematical formula used to calculate the area of a triangle when the lengths of all three sides are known. It does not require knowledge of the height of the triangle.
2. What is the formula used in the calculator?
The calculator uses the following formula:
\[\text{Area} = \sqrt{s(s – a)(s – b)(s – c)}\]
Where:
- \( a, b, c \) are the lengths of the three sides
- \( s \) is the semi-perimeter, calculated as:
\[s = \frac{a + b + c}{2}\]
Final Thoughts: The Heron’s Formula Calculator offers a convenient and reliable way to determine the area of a triangle when only the side lengths are known—no need for height or angle measurements. Whether you’re a student, teacher, engineer, or enthusiast, this tool simplifies complex calculations into a few quick steps. By understanding the principles behind Heron’s formula, you not only gain accurate results but also deepen your knowledge of geometric relationships. Use this calculator to explore triangles confidently and accurately.
My Request to All: If you enjoy using my Heron’s Formula Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
Telegram Link – Join Our Telegram Channel
YouTube Link – Subscribe to Our YouTube Channel
For more tools, please visit our homepage at CalculationClub – Free Online Calculators
For additional tools in Hindi, you can visit MeterToFeet
Thank you for your support!