Perimeter of a Triangle Calculator
The Perimeter of a Triangle Calculator is an advanced online calculator designed to compute not just the perimeter, but a variety of key properties of any triangle based on the information you provide. Whether you enter all three sides (SSS), two sides and an included angle (SAS), two angles and one side (ASA or AAS), or two sides and a non-included angle (SSA), this calculator intelligently adapts to your input.
It accurately calculates the perimeter (P) and can also determine missing sides, angles (α, β, γ). This makes it ideal for students, professionals, and anyone needing quick, reliable triangle calculations.
For a more advanced triangle calculator that also computes heights, medians, inradius, circumradius, and much more, check out our comprehensive tool here: Triangle Calculator.
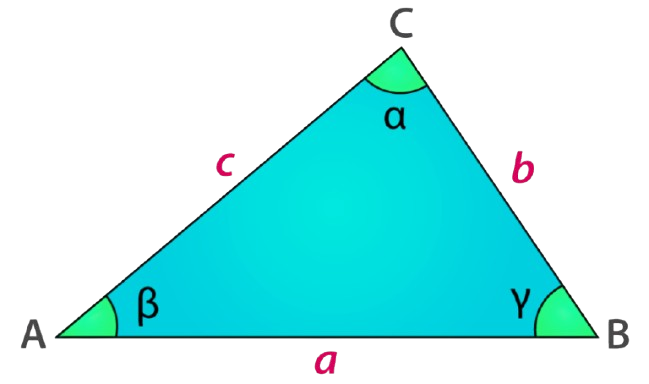
Perimeter of a Triangle?
The perimeter of a triangle is the total length around the triangle — it is simply the sum of the lengths of its three sides.
Formula:
Perimeter = a + b + c
Where:
- a, b, and c are the lengths of the three sides of the triangle.
This calculator can determine the perimeter or an unknown value using any three of the following values: side lengths, angles, or perimeter. A total of 12 valid input combinations are supported, as outlined below.
Supported Input Combinations
- Case 1: Three Sides / Side + Perimeter
- \( a, b, c \rightarrow P \)?
- \( a, b, P \rightarrow c \)?
- \( a, c, P \rightarrow b \)?
- \( b, c, P \rightarrow a \)?
- Case 2: Two Sides + Included Angle
- \( a, b, \gamma \rightarrow P \)?
- \( a, \gamma, P \rightarrow b \)?
- \( b, \gamma, P \rightarrow a \)?
- \( a, b, P \rightarrow \angle \gamma \)?
- Case 3: Two Angles + Included Side
- \( a, \angle \gamma, \angle \beta \rightarrow P \)?
- \( \angle \gamma, \angle \beta, P \rightarrow a \)?
- \( a, \angle \gamma, P \rightarrow \angle \beta \)?
- \( a, \angle \beta, P \rightarrow \angle \gamma \)?
Formula Derivation: Finding the Side b Using Side a, Included Angle γ, and Perimeter
Given:
- Side \( a = a \)
- Included angle \( \gamma = \gamma^\circ \)
- Perimeter \( P = P \)
To Find: Side \( b \)
Formula Used:
\[b = \frac{a^2 – (P – a)^2}{2a \cos(\gamma) – 2(P – a)}\]
Derivation:
- Start with the Law of Cosines:
\[\cos(\gamma) = \frac{a^2 + b^2 – c^2}{2ab}\] - Since the perimeter is \( P = a + b + c \), the third side:
\[c = P – a – b\] - Substitute into the Law of Cosines:
\[\cos(\gamma) = \frac{a^2 + b^2 – (P – a – b)^2}{2ab}\] - Expand \( (P – a – b)^2 \) and simplify:
\[\cos(\gamma) = \frac{a^2 – (P – a)^2 + 2(P – a)b}{2ab}\] - Multiply both sides by \( 2ab \):
\[2ab \cos(\gamma) = a^2 – (P – a)^2 + 2(P – a)b\] - Rearrange to isolate \( b \):
\[b \left[ 2a \cos(\gamma) – 2(P – a) \right] = a^2 – (P – a)^2\] - Solve for \( b \):
\[b = \frac{a^2 – (P – a)^2}{2a \cos(\gamma) – 2(P – a)}\]
Final Answer:
\[\boxed{b = \frac{a^2 – (P – a)^2}{2 \left( a \cos(\gamma) – (P – a) \right)}}\]
Formula Derivation of the Formula for Perimeter
\( P = a + a \times \frac{\sin \beta + \sin \gamma}{\sin(\beta + \gamma)} \)
In any triangle, the sum of interior angles is:
\(\alpha + \beta + \gamma = 180^\circ\)
Using the Law of Sines:
$\frac{a}{\sin \alpha} $$= \frac{b}{\sin \beta} $$= \frac{c}{\sin \gamma} = k$
Expressing sides \(b\) and \(c\) in terms of \(a\):
$b = \frac{a \sin \beta}{\sin \alpha}, \quad c $$= \frac{a \sin \gamma}{\sin \alpha}$
The perimeter \(P\) is the sum of the three sides:
$P = a + b + c$$ = a + \frac{a \sin \beta}{\sin \alpha} + \frac{a \sin \gamma}{\sin \alpha} $$= a + \frac{a}{\sin \alpha}(\sin \beta + \sin \gamma)$
Since \(\alpha = 180^\circ – (\beta + \gamma)\), and \(\sin(180^\circ – x) = \sin x\), we get:
\(\sin \alpha = \sin(\beta + \gamma)\)
Therefore, the perimeter formula becomes:
\[\boxed{P = a + a \times \frac{\sin \beta + \sin \gamma}{\sin(\beta + \gamma)}}\]
Steps to Solve for Unknown Triangle Properties
It uses a mix of geometry rules like:
- Perimeter formula: $P = a + b + c$
- Law of Cosines (for side-angle-side problems)
- Law of Sines (for angle-side-angle or angle-angle-side problems)
- Triangle angle sum rule: $\angle A + \angle B + \angle C = 180^\circ $
1. Using Three Sides (a, b, c):
- Given: all three side lengths
- Find:
- Perimeter: \( P = a + b + c \)
- Missing side if perimeter and two sides are known:
- \( a + b + ? = P \Rightarrow c = P – a – b \)
- Similar for solving for \( a \) or \( b \)
2. Using Two Sides + Included Angle (SAS Case):
- Given: two sides and the angle between them
- Find:
- Third side using Law of Cosines
- Perimeter by summing all sides
- Missing angle if perimeter is known
- Examples:
- \( a, b, \angle γ \Rightarrow P \)?
- \( P, \angle γ, P \Rightarrow a \)?
- \( a, \angle γ, P \Rightarrow b \)?
- \( a, b, P \Rightarrow \angle γ \)?
3. Using Two Angles + One Side (ASA or AAS Case):
- Given: one side and two angles
- Find:
- Third angle using angle sum rule
- Other two sides using Law of Sines
- Perimeter by summing all three sides
- Examples:
- \( a, \angle γ, \angle β \Rightarrow P \)?
- \( a, \angle β, P \Rightarrow \angle γ \)?
- \( \angle γ, \angle β, P \Rightarrow a \)?
- \( a, \angle γ, P \Rightarrow \angle β\)?
Use Cases
- Students solving geometry problems
- Teachers demonstrating triangle rules
- Engineers or architects needing quick perimeter or side estimates
- Designers or surveyors calculating structural lengths
Output Details:
- Triangle Perimeter
- Side Lengths: \( a, b, c \)
- Angles (if angle inputs are included)
- Optionally, Area (if extended to use Heron’s formula)
How to Use the Perimeter of a Triangle Calculator
This calculator allows you to find the perimeter of a triangle or solve for an unknown side or angle using various combinations of inputs. Follow these steps to get started:
1. Select Your Input Type: Use the dropdown menu labeled “Given” to choose one of the following options:
- 3 Sides:
- \( a, b, c \rightarrow P \)?
- \( a, b, P \rightarrow c \)?
- \( a, c, P \rightarrow b \)?
- \( b, c, P \rightarrow a \)?
- 2 Sides + Angle Between:
- \( a, b, \gamma \rightarrow P \)?
- \( a, \gamma, P \rightarrow b \)?
- \( b, \gamma, P \rightarrow a \)?
- \( a, b, P \rightarrow \angle \gamma \)?
- 2 Angles + Side Between:
- \( a, \angle \gamma, \angle \beta \rightarrow P \)?
- \( \angle \gamma, \angle \beta, P \rightarrow a \)?
- \( a, \angle \gamma, P \rightarrow \angle \beta \)?
- \( a, \angle \beta, P \rightarrow \angle \gamma \)?
2. Enter Known Values:
- Input values for sides: a, b, and/or c
- Enter angle values if applicable: γ, β
- Values must be in meters for length and degrees for angles (or adjust units as needed)
3. Choose Decimal Precision:
- Select how many decimal places you want the result to be rounded to (e.g., 3)
- Select Units:
- Length Units: Meters (m), Centimeters (cm), Millimeters (mm), Yards (yd), Feet (ft), Inches (in)
- Angle Units: Degrees (°), Radians (rad)
4. Click “Calculate”: The calculator will compute the perimeter and any unknown side or angle.
5. Hide Steps: Toggle this option to hide or show detailed calculation steps.
6. Reset: Clear all inputs to start a new calculation.

Perimeter of a Triangle Calculator
Example.1 : Calculating the Perimeter of a Triangle When All Sides Are Given
Given the sides of a triangle:
- Side \( a = 2 \) meters
- Side \( b = 3 \) meters
- Side \( c = 4 \) meters
Calculate the Perimeter
Perimeter = a + b + c
P = 2 + 3 + 4
Therefore, the perimeter is:
P = 9 meters
Example 2: Finding Missing Side a When Perimeter is Given
Given the perimeter and two sides of a triangle:
- Perimeter \( P = 18 \) meters
- Side \( b = 6 \) meters
- Side \( c = 5 \) meters
Use the perimeter formula:
\( P = a + b + c \)
\( 18 = a + 6 + 5 \)
\( a = 18 – 11 \)
Therefore, the missing side is: a = 7 meters
Example 3: Finding Missing Side b When Perimeter is Given
Given the perimeter and two sides of a triangle:
- Perimeter \( P = 22 \) meters
- Side \( a = 8 \) meters
- Side \( c = 7 \) meters
Use the perimeter formula:
\( P = a + b + c \)
\( 22 = 8 + b + 7 \)
\( b = 22 – 15 \)
Therefore, the missing side is: b = 7 meters
Example 4: Finding Missing Side c When Perimeter is Given
Given the perimeter and two sides of a triangle:
- Perimeter \( P = 30 \) meters
- Side \( a = 10 \) meters
- Side \( b = 9 \) meters
Use the perimeter formula:
\( P = a + b + c \)
\( 30 = 10 + 9 + c \)
\( c = 30 – 19 \)
Therefore, the missing side is: c = 11 meters
Example 5: Finding the Perimeter of a Triangle when two sides and the included angle are given
Given:
- Side \( a = 2 \) meters
- Side \( b = 3 \) meters
- Included angle \( \gamma = 33^\circ \)
Use Law of Cosines to Find Side \( c \)
The Law of Cosines formula is:
\( c^2 = a^2 + b^2 – 2ab \cos(\gamma) \)
\( c^2 = 2^2 + 3^2 – 2 \times 2 \times 3 \times \cos(33^\circ) \)
\( c^2 = 4 + 9 – 12 \times 0.8387 \)
\( c^2 = 13 – 10.064 = 2.936 \)
Taking the square root to find \( c \):
\( c = \sqrt{2.936} = 1.713 \) meters
Calculate the Perimeter
Perimeter = \( a + b + c = 2 + 3 + 1.713 = 6.713 \) meters
Example 6: Finding Side \( b \) and Side \( c \) Given Perimeter, Side \( a \), and Included Angle \( \gamma \)
Given:
- Perimeter \( P = 9 \) meters
- Side \( a = 2 \) meters
- Included angle \( \gamma = 33^\circ \)
Use Derived Formula to Find Side \( b \)
The formula derived for side \( b \) is:
\[\boxed{b = \frac{a^2 – (P – a)^2}{2 \left( a \cos(\gamma) – (P – a) \right)}}\]
Substitute the values:
b = 4.227 meter
Calculate Side \( c \)
\[ c = P – a – b = 9 – 2 – 4.227 = 2.773 \text{ meters} \]
Example 7: Finding Side \( a \) and Side \( c \) Given Perimeter, Side \( b \), and Included Angle \( \gamma \)
Given:
- Perimeter \( P = 9 \) meters
- Side \( b = 3 \) meters
- Included angle \( \gamma = 33^\circ \)
Use Derived Formula to Find Side \( a \)
The formula derived for side \( a \) is:
\[\boxed{a = \frac{b^2 – (P – b)^2}{2 \left( b \cos(\gamma) – (P – b) \right)}}\]
Substitute the known values:
a = 3.875 meters
Calculate Side \( c \)
c = P – a – b = 9 – 3.875 – 3 = 2.125 meters
Example 8: Calculating Side \( c \) and Angle \( \gamma \) Using Perimeter and Law of Cosines
Given:
- Side \( a = 2 \) meters
- Side \( b = 3 \) meters
- Perimeter \( P = 9 \) meters
Calculate Side \( c \) Using Perimeter
The third side \( c \) can be found by subtracting the known sides from the perimeter:
c = P – a – b = 9 – 2 – 3 = 4 $\text{ meters}$
The Law of Cosines formula to find angle \( \gamma \) is:
\[\cos(\gamma) = \frac{a^2 + b^2 – c^2}{2ab}\]
Substitute the known values:
$\cos(\gamma) = \frac{2^2 + 3^2 – 4^2}{2 \times 2 \times 3} $$= \frac{4 + 9 – 16}{12} $$= \frac{-3}{12} = -0.25$
Find the angle \( \gamma \) by taking the inverse cosine:
$\gamma = \cos^{-1}(-0.25) \approx 104.48^\circ$
Example 9: Calculating the Perimeter Using One Side and Two Angles
Given:
- Side \( a = 2 \) meters
- Angle \( \beta = 44^\circ \)
- Angle \( \gamma = 33^\circ \)
Step 1: Calculate Angle \( \alpha \)
\(\alpha = 180^\circ – \beta – \gamma = 180^\circ – 44^\circ – 33^\circ = 103^\circ\)
Step 2: Use Law of Sines to Find Sides \( b \) and \( c \)
\(\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}\)
\(\frac{2}{\sin(103^\circ)} = \frac{b}{\sin(44^\circ)}\)
\(b = \frac{2 \cdot \sin(44^\circ)}{\sin(103^\circ)} \approx \frac{2 \cdot 0.6947}{0.9744} \approx 1.425\) meters
\(\frac{2}{\sin(103^\circ)} = \frac{c}{\sin(33^\circ)}\)
\(c = \frac{2 \cdot \sin(33^\circ)}{\sin(103^\circ)} \approx \frac{2 \cdot 0.5446}{0.9744} \approx 1.118\) meters
Step 3: Add All Sides to Get Perimeter
\(P = a + b + c = 2 + 1.425 + 1.118 = 4.543\) meters
Or Second Method
Given:
- Side \( a = 2 \) meters
- Angle \( \beta = 44^\circ \)
- Angle \( \gamma = 33^\circ \)
Formula for Perimeter:
\( P = a + a \times \frac{\sin \beta + \sin \gamma}{\sin(\beta + \gamma)} \)
Calculation:
$ P = 2 + 2 \times \frac{\sin 44^\circ + \sin 33^\circ}{\sin 77^\circ} $$= 2 + 2 \times \frac{0.6947 + 0.5446}{0.9744} = 4.5434 \text{ meters}$
Example 10: Finding Side \( a \) Given Perimeter and Two Angles
Given:
- Perimeter \( P = 5 \) meters
- Angle \( \gamma = 33^\circ \)
- Angle \( \beta = 44^\circ \)
Use the Sine Rule-Based Formula to Find Side \( a \)
When two angles and the perimeter are known, side \( a \) can be found using the formula:
\[a = \frac{P}{1 + \frac{\sin(\gamma)}{\sin(\alpha)} + \frac{\sin(\beta)}{\sin(\alpha)}}\]
First, calculate angle \( \alpha \):
\[\alpha = 180^\circ – \beta – \gamma = 180^\circ – 44^\circ – 33^\circ = 103^\circ\]
Now calculate:
- \( \sin(\alpha) = \sin(103^\circ) \approx 0.974 \)
- \( \sin(\gamma) = \sin(33^\circ) \approx 0.545 \)
- \( \sin(\beta) = \sin(44^\circ) \approx 0.695 \)
Plug values into the formula:
$a = \frac{5}{1 + \frac{0.545}{0.974} + \frac{0.695}{0.974}} $$= \frac{5}{1 + 0.559 + 0.713} $$= \frac{5}{2.272} \approx 2.201 \text{ meters}$
Note:
- If you know side a, ∠β, and the perimeter P, and want to find angle ∠γ, use our calculator to see the step-by-step calculation.
- If you know side a, angle ∠γ, and the perimeter P, and want to find angle ∠, use our calculator to see the step-by-step calculation.
Frequently Asked Questions (FAQs) on Perimeter of a Triangle Calculator
1. What is the perimeter of a triangle?
The perimeter of a triangle is the total length around the triangle, calculated by adding the lengths of all three sides:
Perimeter = a + b + c
2. How do I calculate the perimeter if only two sides and the included angle are given?
You can use the Law of Cosines to find the third side, and then add all three sides to find the perimeter:
\( c = \sqrt{a^2 + b^2 – 2ab\cos(\gamma)} \)
3. Can I find the missing side if the perimeter and two sides are given?
Yes, you can rearrange the perimeter formula to solve for the unknown side: \( c = P – a – b \)
4. Does the calculator check if a triangle is valid?
Yes, the calculator applies the Triangle Inequality Theorem, which checks whether the sum of any two sides is greater than the third side.
5. What units can I use in this calculator?
The calculator supports various length units including meters, centimeters, millimeters, feet, inches, and yards. Angles can be input in degrees or radians.
6. Can the calculator show step-by-step solutions?
Yes, the calculator provides step-by-step breakdowns for how the perimeter and missing values are computed.
Final Thoughts: The Perimeter of a Triangle Calculator makes it easy to find the perimeter or missing sides and angles using just a few inputs. Whether you’re using side lengths, angles, or both, it applies the right geometric rules to deliver fast, accurate results—perfect for students, teachers, and professionals alike.
My Request to All: If you enjoy using my Perimeter of a Triangle Calculator and my website, please consider sharing the link to this page or the website with your friends. Additionally, if you have any requests, complaints, suggestions, or feedback, feel free to reach out via our WhatsApp channel or Telegram group.
Telegram Link – Join Our Telegram Channel
YouTube Link – Subscribe to Our YouTube Channel
For more tools, please visit our homepage at CalculationClub – Free Online Calculators
For additional tools in Hindi, you can visit MeterToFeet
Thank you for your support!